METH

Geometry and Quadrilaterals Quiz
Test your knowledge of quadrilaterals, trapezoids, triangles, and their unique properties in this engaging quiz! Whether you are a student, teacher, or just a geometry enthusiast, this quiz will challenge your understanding of various geometric concepts.
Featuring:
- 40 challenging multiple-choice questions
- Insights on properties and theorems
- Fun and educational experience
Opposite sides are parallel, Opposite sides are congruent, Opposite angles are congruent, Diagonals bisect each other, Any pair of consecutive angles are supplementary. These are properties of what?
QUADRILATERALS
PARALLELOGRAMS
SHAPES
DRAWINGS
All legs are congruent, Legs are congruent by definition, Bases are parallel by definition, Lower base angles are congruent, Upper base angles are congruent, Diagonals are congruent, Any lower base angle is supplementary to any upper base angle. These are properties of what?
ISOSCELES SQUARE
ISOSCELES CONE
ISOSCELES TRAPEZOID
ISOSCELES TRIANGLE
What the do you call the line segment that joins the midpoints of the non-parallel sides?
MIDLINE
MEDIAN
MEAN
MODE
½(b + b₂) WHAT IS THIS FORMULA FOR?
FOR AREA OF TRAPEZOID
FOR MEDIAN OF TRAPEZOID
FOR AREA OF KITE
FOR MIDLINE OF TRIANGLE
Properties of a parallelogram apply by definition, All angles are right angles, Diagonals are congruent. WHAT QUADRILATERAL HAS THESE PROPERTIES
SQUARE
CIRCLE
RECTANGLE
RHOMBUS
Properties of a parallelogram apply by definition, Two consecutive sides are congruent by definition, Sides are congruent, Diagonals bisect the angles, Diagonals are perpendicular bisectors of each other, Diagonals divide the rhombus into four congruent right triangles. WHAT QUADRILATERAL HAS THESE PROPERTIES?
QUADRILATERAL
SQUARE
PARALLELOGRAM
RHOMBUS
Properties of a rectangle apply by definition, Properties of a rhombus apply by definition, Diagonals form four isosceles right triangles. WHAT QUADRILATERAL HAS THESE PROPERTIES?
RHOMBUS
CIRCLE
OVAL
SQUARE
Has two distinct pairs of consecutive sides of the same length, Two disjoint pairs of consecutive sides are congruent by definition, Diagonals of a kite are perpendicular to each other, One diagonal is the perpendicular bisector of the other, One of the diagonals bisect a pair of opposite angles, A pair of opposite angles are congruent. WHAT QUADRILATERAL HAS THESE PROPERTIES?
KITE
SQUARE
RECTANGLE
TRIANGLE
A = ½dd₂, WHAT IS THIS FORMULA USED FOR?
AREA OF KITE
AREA OF SQUARE
AREA OF PARALLELOGRAM
AREA OF TRAPEZOID
A = ½dd₂, IN THIS FORMULA, WHAT DOES THE D STAND FOR?
DIAGONAL
DERIVATIVE
DI KA NIYA CRUSH
DI KA PAPASA SA PERIO
Both pairs of opposite sides are congruent and parallel, Diagonals bisect each other, Both pairs of opposite angles are congruent, Consecutive angles are supplementary. THESE ARE CONDITIONS THAT GUARANTEE THAT A QUADRILATERAL IS A?
PARALLELOGRAM
QUADRILATERAL
SQUARE
SHAPE
The median of a trapezoid is half of the sum of its bases, The base angles of an isosceles trapezoid are congruent, Opposite angles of an isosceles trapezoid are supplementary, The diagonals of an isosceles trapezoid are congruent. THESE ARE THEOREMS OF WHAT?
THEOREMS ON TRAPEZOIDS
THEOREMS ON TRIANGLES
THEOREMS ON SQUARES
RIGHT TRIANGLE THEOREM
EFGH is a trapezoid with median IJ. If HG = 12 cm THE UPPER BASE and IJ =15 cm, what is EF THE LOWER BASE?
18
16
9
11
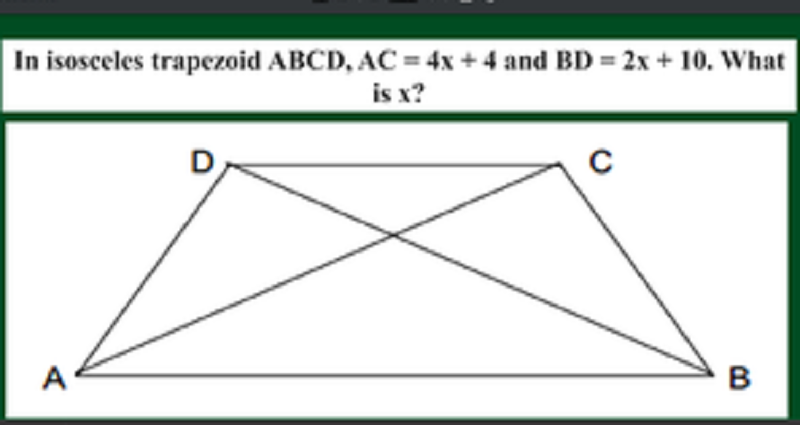
FIND X
3
4
5
6
1. The diagonals are perpendicular to each other. 2. The area is half of the product of its diagonals. THESE ARE THEOREMS OF WHAT?
KITE
SQUARE
RHOMBUS
RECTANGLE
Corresponding segments are proportional if the segments of one figure have the same ratio as the segments of the other. WHAT IS BEING DESCRIBED?
PROPORTIONAL SEGMENTS
CORRESPONDING SEGMENTS
CONGRUENT SEGMENTS
LINE SEGMENTS
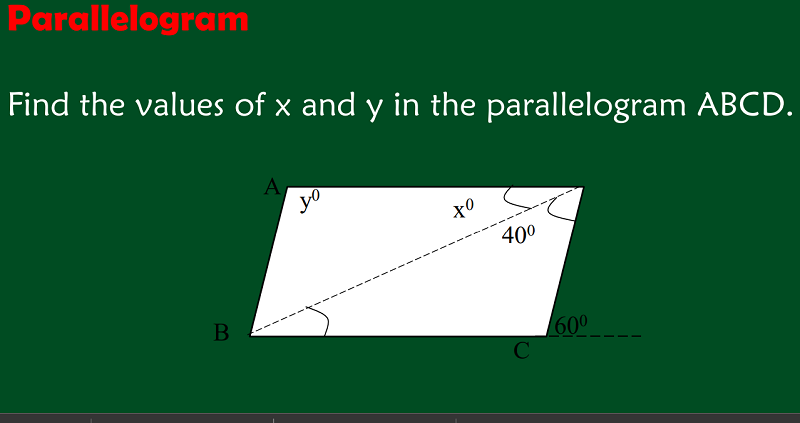
WHAT IS X?
20
40
60
80
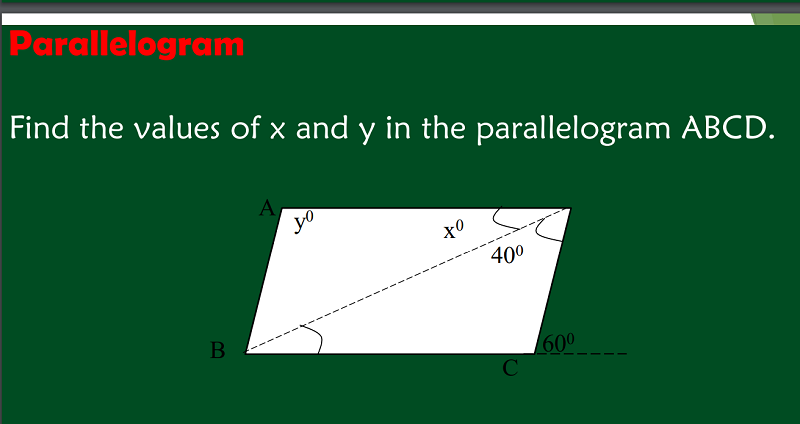
WHAT IS Y?
120
160
180
360
If line segment MAT=6 is proportional to HYP=30, where MA=1 is proportional to HY=5 and then what is YP if its proportional to AT=5?
25
30
5
26

WHAT REASONING IS NUMBER 1?
DEFINITION OF PARALLELOGRAMS
GIVEN
SAS CONGRUENCE POSTULATE
REFLEXIVE PROPERTY

WHAT REASONING IS NUMBER 2?
AIA ARE CONGRUENT
AAA ARE CONGRUENT
VERTICAL ANGLES ARE CONGRUENT
AEA ARE CONGRUENT

WHAT REASONING IS NUMBER 3?
DISTRIBUTIVE PROPERTY
REFLEXIVE PROPERTY
MIRROR PROPERTY
DIAGONAL LINE THAT CUTS PARALLELOGRAM IS CONGRUENT TO ITSELF

WHAT REASONING IS NUMBER 4?
SAS CONGRUENCE POSTULATE
SSS CONGRUENCE POSTULATE
ASS CONGRUENCE POSTULATE
AAA CONGRUENCE POSTULATE
The segment that joins the midpoints of two sides of a triangle is parallel to the third side and half as long. IS WHAT THEOREM?
MIDLINE THEOREM
MEDIAN THEOREM
MEAN THEOREM
MODE THEOREM
Triangles are similar if:
Corresponding Angles are congruent.
Corresponding Sides are not equal
Corresponding Angles are supplementary
Corresponding Angles are vertical.
Triangles are similar if:
Corresponding Sides are proportional
Corresponding Sides are parallel
Corresponding Sides are out of proportion
Corresponding Sides are not real
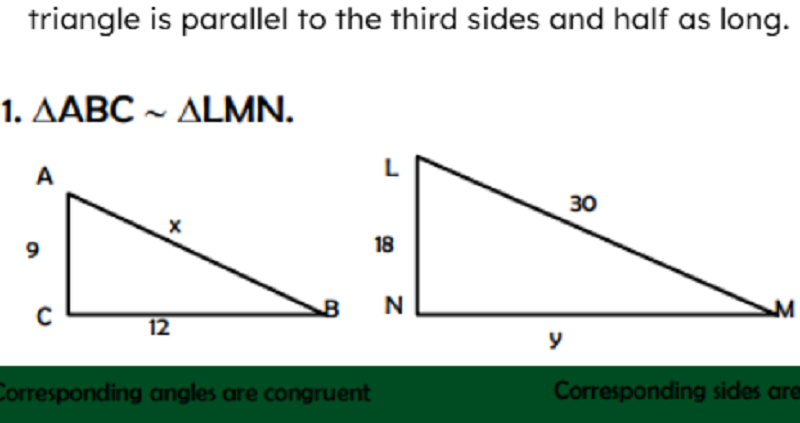
What is x and y?
X=15 and y=5
X=5 and y=13
X=15 and y=24
X=6 and y=9
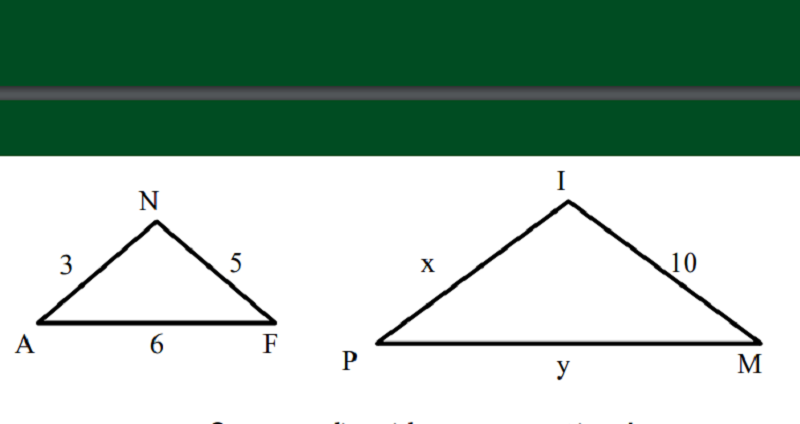
What is x and y?
X=5 and y=10
X=6 and y=12
X=6 and y=-12
X=12 and y=6
If a line is parallel to one side of a triangle and intersects the other two sides, the line divides those sides proportionally. WHAT THEOREM DOES THIS BELONG TOO?
PROPORTIONAL SEGMENTS AND BASIC PROPORTIONALITY THEOREMS
SIMILAR TRIANGLE THEOREMS
AA/AAA Theorem states that if two angles of one triangle are congruent to the two angles of another triangle, then the 2 triangles are similar. WHAT THEOREM DOES THIS BELONG TOO?
PROPORTIONAL SEGMENTS AND BASIC PROPORTIONALITY THEOREMS
SIMILAR TRIANGLE THEOREMS
SAS Theorem states that if in two triangles, two pairs of corresponding sides are proportional and the included angles are congruent, then the triangles are similar. WHAT THEOREM DOES THIS BELONG TOO?
PROPORTIONAL SEGMENTS AND BASIC PROPORTIONALITY THEOREMS
SIMILAR TRIANGLE THEOREMS
If three or more parallel lines are cut by two or more transversals, then the segments cut off by the transversals are proportional. WHAT THEOREM DOES THIS BELONG TOO?
PROPORTIONAL SEGMENTS AND BASIC PROPORTIONALITY THEOREMS
SIMILAR TRIANGLE THEOREMS
The bisector of an angle of a triangle divides the opposite side into segments whose lengths are proportional to the lengths of the adjacent sides. WHAT THEOREM DOES THIS BELONG TOO?
PROPORTIONAL SEGMENTS AND BASIC PROPORTIONALITY THEOREMS
SIMILAR TRIANGLE THEOREMS
SSS Theorem states that if in two triangles, three corresponding sides are proportional, then the triangles are similar. WHAT THEOREM DOES THIS BELONG TOO?
PROPORTIONAL SEGMENTS AND BASIC PROPORTIONALITY THEOREMS
SIMILAR TRIANGLE THEOREMS
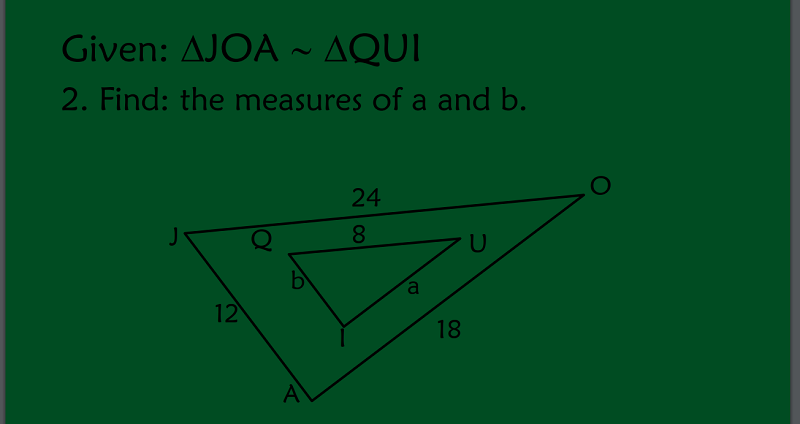
WHAT IS A AND B?
A=6 AND B=4
A=-6 AND B=-4
A=4 AND B=6
A=3 AND B=5
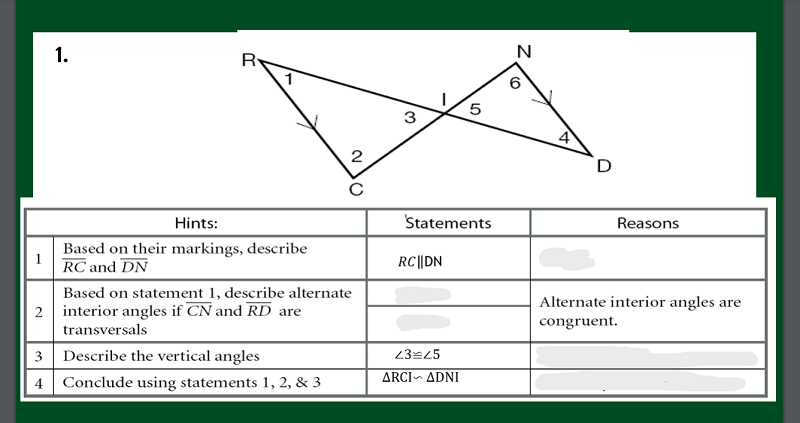
WHAT IS THE REASONING FOR NUMBER 1? BASED ON THE DRAWING
GIVEN
AIA ARE CONGRUENT
SAS CONGRUENCE POSTULATE
REFLEXIVE PROPERTY
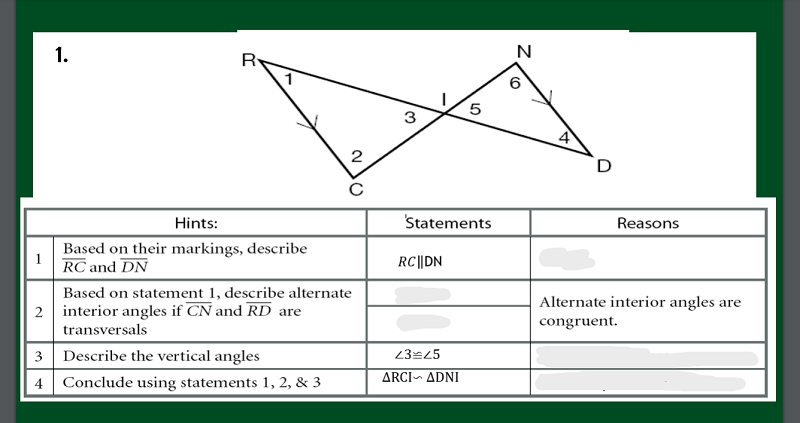
WHAT IS THE STATEMENT IN NUMBER 2?
�1≌∠4 AND ∠2≌∠6
�1≌∠3 AND ∠2≌∠5
�2≌∠4 AND ∠1≌∠6
�1≌∠1 AND ∠2≌∠2
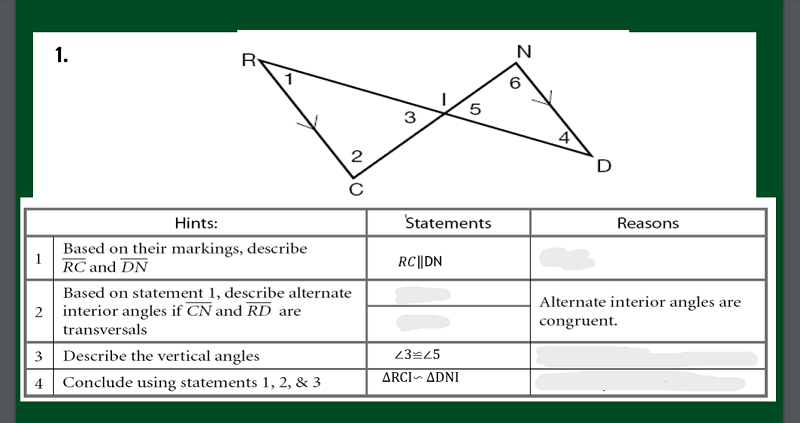
WHAT IS THE REASONING FOR NUMBER 3?
VERTICAL ANGLES ARE CONGRUENT
DIAGONAL ANGLES ARE CONGRUENT
INTERIOR ANGLES ARE CONGRUENT
VERTICAL ANGLES ARE NOT CONGRUENT
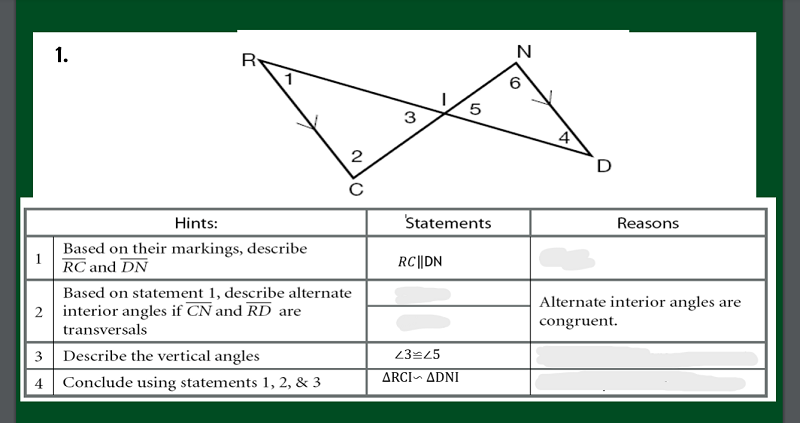
WHAT IS THE REASONING FOR NUMBER 4?
SIMILARITY POSTULATE SS/SSS
SIMILARITY POSTULATE AA/AAA
SIMILARITY POSTULATE SA/SAS
SIMILARITY POSTULATE AS/ASS
{"name":"METH", "url":"https://www.quiz-maker.com/QPREVIEW","txt":"Test your knowledge of quadrilaterals, trapezoids, triangles, and their unique properties in this engaging quiz! Whether you are a student, teacher, or just a geometry enthusiast, this quiz will challenge your understanding of various geometric concepts. Featuring: 40 challenging multiple-choice questions Insights on properties and theorems Fun and educational experience","img":"https:/images/course5.png"}
More Quizzes
Triangle Similarity and Area Ratio Quiz
1059
Math-Quiz
11614
DEIJ-January Employee Quiz
940
Biyokimya
381933
LED Lighting Product Knowledge - Free Online
201017223
Steampunk Name Generator - Free to Find Yours
201018557
Skull and Bones - Free Skeletal System Challenge
201019471
Hard Pokémon - Prove Your Trainer Mastery
201020724
Air Force Ranks - Free Practice Online
201017160
Which Good Doctor Character Are You? Free
201017482
Solutes and Solvents Quick Check - Free Online
201015922
Order of Draw for Phlebotomy - Tube Sequencing
201019041