Od kviza do kodovanja
Od kviza do kodovanja
Testirajte svoje znanje o kodiranju i komunikacionim kanala uz naš interaktivan kviz! Ovaj kviz sadrži 30 pitanja koja pokrivaju razliĝite aspekte kodiranja, ukljuĝujući LDPC kodove, konvolucione kodove, i teoriju informacija.
Uĝestvujući u kvizu, nauĝićete:
- O znaĝaju kapaciteta kanala
- Kako funkcioniraju cikliĝni i blok kodovi
- Primjene kodova u razliĝitim tehnologijama
(*)Ukoliko primenimo kod ponavljanja, dovoljno velik broj ponavljanja:
U stanju smo da kompenzujemo gubitke usled sumova na kanalu do mere koja je definisana kapacitetom kanala
U stanju smo da kompenzujemo gubitke usled sumova na kanalu do proizvoljne mere
(*)DMC komunikacioni kanal je vremenski:
Nepromenljiv
Promenljiv
(*)Sta je polinomska reprezentacija reci 11001?
X^3+X^2
Nijedan od ponudjenih odgovora
X^4+0
X^4+1
(*)Sindrom kodna rec zavisi samo od greske, a ne I od emitovane kodne reci:
Ovo vazi kod ciklicnih kodova
Ovo vazi kod sifarskih kodova
Ovo vazi kod blok kodova
(*)Izrazom Pb >= h^~-1(1-C/R) definisana je verovatnoca greske na izlazu kanala:
Bez upotrebe povratne sprege
Ne zavisi od povratne sprege
Sa upotrebom povratne sprege
(*)Binarna suma bita poruke za poruku 01001 je:
0
1
(*)Hibridni ARQ:
Detektuje ali ne ispravlja gresku
Detektuje I ispravlja gresku
(*)Kraftova nejednakost potvrdjuje postojanje:
Senon - Fanoovog prefiksnog koda
Ocekivane duzine koda
Prefiksnih kodova datog komunikacionog kanala
(*)Kada se jedna kodna rec Zi prenosi po nekom kanalu sa sumovima I na izlazu kanala primi Z', tada se odgovarajuca greska u prenosu dobija kao:
Razlika e = Zi - Z'
Zbir e = Z' + Zi
Razlika e = Z' - Zi
(*)Kod konvolucionih kodova krace kodne reci se izjednacavaju prema duzoj:
Dodavanjem nula na kraju
Dodavanjem jedinica
Dodavanjem nula I jedinica
(*)Da li je tvrdjenje tacno: Vektorski prostori su u pogledu algebarske strukture kompletnije od ciklicnih kodova:
Netacno
Tacno
Nije uporedivo
(*)Senon je svojim radom ,,A mathematical theory of communication" iz 1948. Objasnio ako je brzina ispod kapaciteta kanala:
Povecanje pouzdanosti prenosa se moze u potpunosti ostvariti konstrukcijom kompleksnijih sistema kodovanja I dekodovanja, bez potrebe da se menja odnos signal/sum
Povecanje pouzdanosti prenosa se ne moze u potpunosti ostvariti konstrukcijom kompleksnijih sistema kodovanja I dekodovanja, bez promene odnosa signal/sum
(?)Kod verovatnosnog n-arnog stabla:
Moguce je sracunati verovatnoce unutrasnjih cvorova
Moguce je sracunati verovatnoce unutrasnjih cvorova samo ukoliko je izvor diskretan
Nije moguce sracunati verovatnoce unutrasnjih cvorova
Nijedan od ponudjenih odgovora nije tacan
(*)Ako je z kodna rec koja se prenosi, a e greska prilikom prenosa, primljena rec je:
Z = z + H
Z = z + e
Z = z + G
Kod Hafmanovog koda broj neiskoriscenih listova u kodnom stablu koje odgovara optimalnom D-arnom prefiksnom kodu izvora U sa n simbola je jednak:
Pozitivnom ostatku deljenja n-1 sa D-1
Negativnom ostatku deljenja n-1 sa D-1
(*)Posmatrajmo dve kodne reci z1=1010 I z2=0101 jednog ciklicnog koda, sta je onda z1*z2?
101110, mod(X^4-1)
101111, mod(X^4-1)
0, mod(X^4-1)
(*)Na prijemu kodne reci se:
Deinterlivinguju pre dekodovanja
Interlivinguju pre kodovanja
Interlivinguju pre dekodovanja
(*)Svaki linearni kod:
Je pravilan ako ima isti broj nula I jedinica
Sadrzi nula kodnu rec
Ne sadrzi nula kodnu rec
(*)Da bi blok kod mogao da ispravlja 3 greske, njegovo minimalno rastojanje mora biti barem:
7
1
3
Hafmanov algoritam kodovanja izvora informacija bez memorije, pomocu D-arnog prefiksnog koda daje:
Optimalan kod minimalne moguce ocekivane vrednosti kodnih reci
Optimalan kod maksimalne moguce ocekivane vrednosti kodnih reci
(*)Tezina reci 0001100 je:
2
1
(*)Tezina kodnih reci je uvek:
Veca od nule
Veca ili jednaka nuli
Pozitivna ili razlicita od nule
(*)Binarni Hemingov kod pripada grupi:
Ciklicnih kodova
Linearnih kodova
(*)Kapacitet kanala:
Odredjuje deo kanala u kom sum ne deluje na informacije
Meri sposobnost jednog kanala da prenosi informacije
Senon Fanov kod:
Bolji je sto je entropija izvora manja
Ne zavisi od entropije
Bolji je sto je entropija izvora veca
(*)Blokovi velikih duzina LDPC koda:
Rezultuju sa malom verifikacionom I generator matricom
Rezultuju sa malom verifikacionom I malom generator matricom
Rezultuju sa velikom verifikacionom I generator matricom
(*)Ako je R<C sigurni smo da postoji kod:
Cija je greska dekodovanja bita Pb po zelji mala
Ciji je BER uvek manji od 0.01
Cija je greska dekodovanja bita Pb uvek veca
(*)Resetka dimenzije m konvolucionog koda (n, k, r) predstavljaju:
Putanje u dijagramu stanja iste duzine razvijene u prostoru
Putanje u dijagramu stanja iste duzine razvijene u vremenu I prostoru
Putanje u dijagramu stanja iste duzine razvijene u vremenu
Putanje u dijagramu stanja razlicite duzine razvijene u vremenu
Kod Hafmanovog koda broj listova u D-arnom stablu je:
1+k(D-1), gde je k broj unutrasnjih cvorova, ne ukljucujuci koren
1+2(D-2), gde je k broj unutrasnjih cvorova, ukljucujuci koren
1+k(D-1), gde je k broj unutrasnjih cvorova, ukljucujuci koren
(*)Konvolucioni koder je masina stanja(state machine). Rad takvih sistema je odredjen:
Dijagramom stanja
Polinomom stanja
Polinomnom konvoluciom
(*)Linearni kodovi predstavljaju jednu od najznacajnijih klasa kodova zbog njihove:
Kompleksnosti
Duzine
Kompleksne implementacije
Jednostavnosti
Za bilo koji diskretni izvor informacija bez memorije, cija je entropija H(U):
Postoji logD, D-arni prefiks kod
Postoji barem jedan D-arni prefiks kod
(*)Za kanal kazemo da je bez povratne sprege ukoliko raspodela verovatnoce:
Ulaza ne zavisi od izlaza
Ulaza zavisi od izlaza
(*)RS kodovi pogodni su za ispravljanje:
Koncentrisanih, paketnih gresaka
Nekoncentrisanih, pojedinacnih gresaka
(*)Dualni kod dualnog koda C je:
Kod C
Verifikaciona matrica
Generator Matrica
(*)Tanerovi grafovi za reprezentaciju LDPC koda su:
Kompleksni
Simetricni
Biparitetni
Paritetni
(*)Hemingovo rastojanje dve kodne reci jednako je broju nultih pozicija njihove razlike:
Tacno
Netacno
(*)D-arni blok kod duzine n je:
Prazan skup vektorskog prostora n-torki GF(D)^(n-1)
Pun podskup vektorskog prostora n-torki GF(D-1)^n
Nijedan od ponudjenih odgovora
(*)Sta je polinomska reprezentacija reci 11001:
X^4+0
X^3+X^2
X^4+1
Nijedan od ponudjenih odgovora
(*)Moze se reci da konvolucioni kodovi:
Daju bolje rezultate od blok kodova
Daju losiji rezultat od blok kodova
(*)Generator ciklicnog koda duzine n je faktor polinoma:
X^n-1
X^n+1
X^n-2
(*)Ako je z(X) polinom koji odgovara kodnoj reci z ciklicnog koda duzine n, tada svaki polinom p(x), p(x)*z(x) mod(X^n -1) odgovara polinomu cija je odgovarajuca kodna rec pripada:
Istom ciklicnom kodu (ciklicni pomeraj u levo plus linearne kombinacije)
Drugom ciklicnom kodu (ciklicni pomeraj u levo plus linearne kombinacije)
Istom ciklicnom kodu (ciklicni pomeraj u desno plus linearne kombinacije
(*)Kod koda ponavljanja verovatnoca pogresnog dekodovanja tezi nuli, kada:
Smanjujemo duzine kodnih reci
Povecavamo duzine kodnih reci
(*)Detektovanje greske ekvivalentno je sa detektovanjem nenulte tezine kodne reci.
Tacno
Netacno
(*)Povratna sprega ima znacenje kada je:
R<C
R>C
(*)Jebote kolki tekst, pa'i sad ovo: Blok kod duzine n I dekodovanjem minimalnog rastojanja, moze za bilo koja dva broja t I s, da ispravi sve oblike nizova gresaka sa ukupno t ili manje gresaka I da detektuje sve oblike nizova gresaka sa t+1,...,t+s gresaka, ako I samo ako je minimalno rastojanje koda striktno:
Vece od 2t-s
Vece od 2t+s
(*)Opsta procedura dekodovanja primljene poruke je sledeca:
Izracunati sindrom, izracunati korektor, izvrsiti dekodovanje
Izracunati korektor, izvrsiti dekodovanje, izracunati sindrom
Izvrsiti dekodovanje, izracunati sindrom, izracunati korektor
(?)Kodne reci su sekvence simbola iz kodnog alfabeta:
Koji je u opstem slucaju razlicit od alfabeta poruka
Koji je u opstem slucaju isti alfabetu iz poruke
(*)Najmanja kolicina sifrata koja omogucava da sistem bude razbijen naziva se:
Tacka nejedinstvenosti
Tacka podudarnosti
Kriticna tacka sifre
Tacka jedinstvenosti
Za jedan kod se kaze da je _________ ako u njemu nijedna kodna rec nije prefiks nekoj drugoj kodnoj reci.
Prefiksan
Sufiksan
(*)Konkatenacija je:
Kovolucija dva ili vise kodova za ispravljanje gresaka
Kombinovanje dve kodne reci ili vise kodnih reci zbog bolje interlivinga
Kombinovanje tri kodne reci ili vise kodnih reci zbog boljeg interlivinga
(*)Brzina konvolucionog koda je:
1/4
1/6
1/2
(*)U procesu dekodovanja kod ciklicnih kodova prvo izracunavamo:
Koretkor
Lektor
Generator matricu
Hemingovu matricu
Sindrom
(*)Generator matrica jednog koda je verifikaciona matrica njegovog dualnog koda I obrnuto.
Netacno
Tacno
(*)Stoga je nalazenje raspodele verovatnoce ulaza za koju se dostize kapacitet simetricnog DMC kanala:
Ekvivalentno nalazenju ulaza koji maksimizuje neodredjenost izlaza
Ekvivalentno nalazenju ulaza koji maksimizuje odredjenost izlaza
(?)Nivo suma je takav:
Da je moguce preneti poruke sa prihvatljivim nivoom gresaka u prenosu
Da nije moguce preneti gde je odnos snage signala I suma negativna vrednost
(*)I(C;M) = 0, oznacava da je:
Sifarski sistem perfektan
Sifarski sistem diskretan
Sifarski sistem jednoznacan
(*)Posmatrajmo dve kodne reci z1=010110 I z2=000100 jednog ciklicnog koda, sta je onda z1*z2?
11000101, mod(x^6-1)
011001, mod(x^6-1)
111001, mod(x^6-1)
(*)Kod binarnog Hemingovog koda minimalno rastojanje je uvek:
1
3
2
(*)Kod dekodovanja minimalnog rastojanja I maksimalne verodostojnosti, minimizacija je ekvivalentna nalazenju najblize kodne reci u odnosu na:
Poslatu
Primljenu
(*)Verifikaciona matrica binarnog linearnog koda:
Nema nula kolonu
Ima nula kolonu
(*)Ciklicna permutacija kodne reci kod ciklicnih kodova je:
Sindrom rec
Kodna rec
Generator matrica
(*)Ukoliko kod koda ponavljanja konstantno uvecavamo n:
Brzina prenosa postaje neprihvatljiva
Brzina prenosta ostaje prihvatljiva
(*)Ako je kapacitet jednog DMC, C=0.25 bita za prenos poruka BSS izvora, ako se prenos vrsi brzinom R=0.5, tada dobijamo gresku najmanje 11%, sto znaci:
Da ce najmanje 11% bita biti pogresno dekodovano ako ne koristimo kod za ispravljanje gresaka
Da ce najmanje 11% bita biti pogresno dekodovano bez obzira kakav kod za ispravljanje gresaka primenili
Kodovanje radi kompresije predstavlja:
Odbacivanje redudanse
Dodavanje redudanse
(*)Matrica H3 = [0001111; 0110011; 1010101] je H matrica Hemingovog koda za r=
2
4
3
(*)Ciklicni kodovi pripadaju klasi:
Nelinearnih kodova
Konvolucionih kodova
Blok kodova
Linearnih kodova
(*)Koja tvrdnja je tacna?
FEC je daleko jednostavnije dekodovanje u poredjenju sa ARQ
HARQ je daleko jednostavnije dekodovanje u poredjenju sa ARQ
ARQ je daleko jednostavnije dekodovanje u poredjenju sa FEC
ARQI je daleko jednostavnije dekodovanje u poredjenju sa FEC
(*)Nacin za korigovanje paketskih gresaka je:
Intermove
Interliving
Interdivide
(*)Brzina koda sa ponavljanjem srazmerna je (n- broj ponavljanja):
Reciprocnoj vrednosti broja ponavljanja
1*n
2/n
(*)Broj algoritama za dekodovanje LDPC koda je:
1
4
2
3
(?)Cilj teorije kodovanja je dizajniranje:
Idealnoj prijemnika u komunikacionom sistemu
Kodova sto vece brzine I sto manje greske dekodovanja
Kodova sto manje brzine da bi se smanjio procenat gresaka I pojednostavilo dekodovanje
(*)Kod ciklicnih kodova:
Nula kodna rec se koduje jedinice kodnu rec
Nula kodna rec se koduje u nula kodnu rec
Nula kodna rec se ne koduje u nula kodnu rec
(*)Korisno za Viterbijev algoritam je svojstvo da je broj najboljih putanja za svaki vremenski korak:
Uvek veci ili razlicit od broja stanja kodera
Uvek manji ili jednak broju stanja dekodera
Uvek manji ili jednak broju stanja kodera
(*)Maksimalni kapacitet ispravljanja gresaka definisan je izrazom:
(d min (C)+1)/2
(d min (C)-1)-1
(d min (C)-1)/2
(*)Hemingovo rastojanje izmedju 10101 I 11101:
Nijedan od ponudjenih odgovora
Nije definisano
4
(?)Hafmanov algoritam konstruise:
Vise optimalnih kodova
Kodne reci
Jedan optimalni kod
(*)Koju klasu predstavljaju LDPC kodovi?
Klasu neliarnih blok kodova
Klasu linearnih blok kodova
Binarni kod
(?)Kolika je tacka jedinstvenosti kriptosistema kojim se sifruju poruke iz alfabeta od 96 znakova, pri cemu je entropija poruka 3 bita po znaku, dok je entropija kljuca 33 bita?
9.9
9.2
58
(*)Kod linearnih kodova:
Moguce je izracunati minimalno rastojanje na osnovu verifikacione matrice
Nije moguce izracunati minimalno rastojanje na osnovu verifikacione matrice
(*)Matrica H dimenzije (n-m) x n je verifikaciona matrica za:
Generator matricu
(n, m) D-arni linearni kod C
(*)Upotrebom povratne sprege u slucaju kada je R manje od C:
Ne pomaze kodovanju I dekodovanju, samim tim nemamo kontrolu nad greskom
Pojednostavljujemo kodovanje, dekodovanje I lakse kontrolisemo gresku
(*)Kolika je brzina prenosa linearnog (n, m) koda:
R = log n/m
R = n/m
R = log m/n
R = m/n
(?)Ako je alfabet beskonacan:
Informacioni izvor je kontinualan
Informacioni izvor je diskretan
Informacioni izvor je odlican
Informacioni izovr je stacionaran
(*)Diskretni kanal bez memorije je najjednostavniji komunikacioni kanal koji je formalno odredjen sa:
Tri velicine
Dve velicine
Cetiri velicine
(*)Svaki linearni kod:
Sadrzi nula kodnu rec
Je pravilan ako ima isti broj nula I jedinica
Ne sadrzi nula kodnu rec
(*)Kod ARQ, NAK predstavlja
Negativnu potvrdu
Laznu potvrdu
HMAC potvrdu
Pozitivnu potvrdu
FAC potvrdu
Da li trenutno dekodivi kodovi zahtevaju memorisanje prispelih kodnih reci ili cekanje dospece novih da bi dekodovanje bilo obavljeno?
Zahtevaju memorisanje po principu CRC
Zahtevaju memorisanje zbog jednoznacnog kodovanja
Ne zahtevaju memorisanje
(?)[quot, remd] = gfdeconv(b, a, p), navedena funckija iz matlaba jebenog predstavlja funckiju za
Deljenje dve promenljive tipa int
Nijedan od ponudjenih odgovora
Deljenje tri polinoma
Deljenje jednog polinoma
(*)Viterbijev algoritam:
Linearne kompleksnosti
Nelinearne kompleksnosti
Eksponencijalne kompleksnosti
(?)Broj grana koje napustaju svako od stanja trelisa:
Odredjen je iskljucivo brojem bitove koji se prenosi
Odredjen je iskljucivo brojem ulaza konvolucionog kodera
Odredjen je iskljucivo brojem stanja konvolucionog kodera
(*)Kada (n, m) linearni kod koristi sistematsku formu generator matrice, tada je prvih m simbola od ukupno n simbola kodne reci egzaktno:
Jednak simbolima poruke
Razlicit simbolima poruke
(?)Kraftova nejednakost nam daje informaciju:
Uslov za postojanje prefiksnog koda
Kada se moze dekodovati neki prefiks kod
Kada ne moze postojati jedan prefiks kod
(*)FEC:
Dekodovanje primljene sekvence kao najblize kodne reci
Automatsko izdavanje zahteva za slanje stare poruke
Automatsko izdavanje zahteva za slanje nove poruke
Dekodovanje primljene sekvence kao najdalje kodne reci
(*)Izabrati nazive algoritama za dekodovanje LDPC koda:
Hard-decision
Slow-decision
Soft-decision
Fast-decision
(*)Minimalna tezina jednog konvolucionog koda jednaka je:
Minimalnom broju nenultih simbola na putanji koja polazi I zavrsava se u nultom stanju
Minimalnom broju nultih simbola na putanji koja polazi I zavrsava se u nenultom stanju
Minimalnom broju nenultih simbola na putanji koja ne polazi I ne zavrsava se u nultom stanju
Minimalnom broju nenultih simbola na putanji koja polazi I ne zavrsava se u nultom stanju
(*)
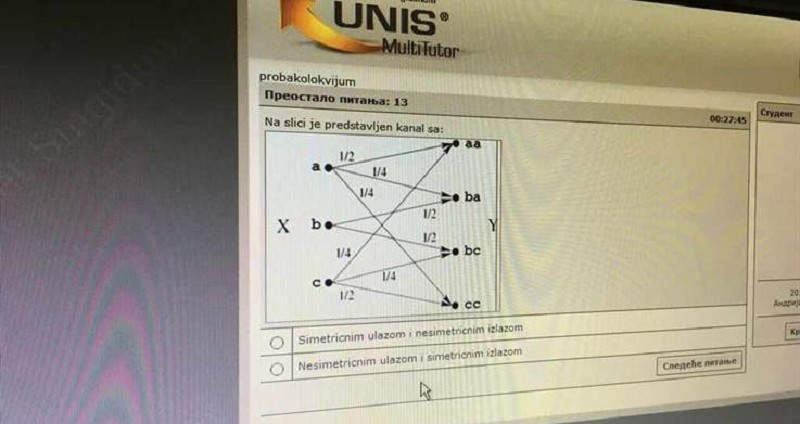
Simetricnim ulazom I nesimetricnim izlazom
Nesimetricnim ulazom I simetricnim izlazom
(*)
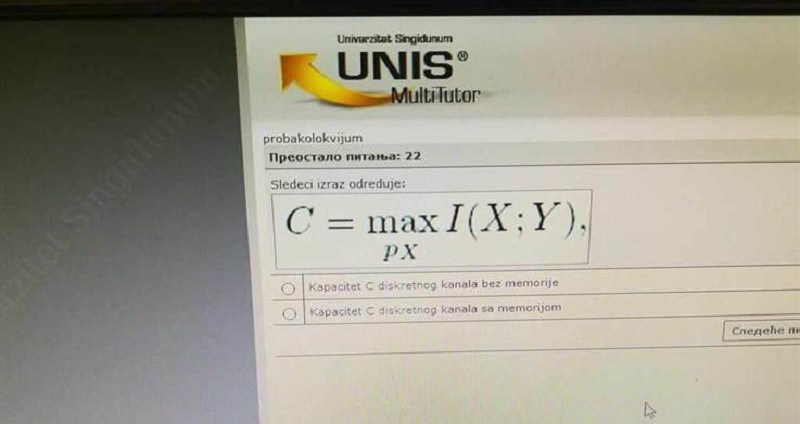
Kapacitet C diskretnog kanala bez memorije
Kapacitet C diskretnog kanala sa memorijmo
(*)Kljucna ideja algebarskog kodovanja je dodavanje:
Algebarske strukture u skupu kodnih reci tako da se greska moze lako izraziti pomocu operacija koje deifnisu tu algebarsku strukturu
Redudansne strukture u sklopu kodnih reci tako da se greska moze lako izraziti pomocu operacija koje definisu kolicinu redudanse
(*)Kapacitet kanala je:
Maksimalna prosecna kolicina informacija koje ulaz kanala moze preneti na izlaz
Maksimalna prosecna kolicina informacija koje ulaz kanala ne moze preneti na izlaz
(*)Na osnovu minimalnog rastojanja postoji nacin da se unapred za zadati kod:
Moze reci koliko gresaka moze detektovati, a koliko ispraviti
Moze reci koliko gresaka moze detektovati, a ne koliko ispraviti
(*)ARQ:
Automatsko izdavanje zahteva za ponavljanjem poruke
Automatsko izdavanje zahteva za kraj komunikacije
Automatsko izdavanje zahteva za slanje nove poruke
(*)Metoda dekodovanja soft-decision predstavlja poseban dizajn LDPC dekodera koji prima:
Sekvencu verovatnoca, umesto binarne sekvence
Binarnu sekvencu, umesto sekvence verovatnoca
Decimalnu sekvencu, umesto sekvence verovatnoca
(*)Blok kod sa minimalnim rastojanjem 8, t-3 I s-1:
Ispravljanje 3 greske I detektovanje 4 greske
Ispravljanje 3 greske I detektovanje 5 greske
Ispravljanje 3 greske I detektovanje 1 greske
(*)Hemingovo rastojanje zadovalja tri aksioma metrickog rastojanja:
Nejednakost trougla
Nulto rastojanje
Simetrija
Jednakost trougla
Geometrija
Jedinicno rastojanje
(*)DMC je simetrican ako je istovremeno sa simetricnim ulazom I sa nesimetricnim izlazom:
Tacno
Netacno
(*)Binarni kod sa 8 kodnih reci(m) I duzinom kodnih reci 6(n) brzina prenosa je:
8/6
6/8
Nijedan od ponudjenih odgovora
(*)LDPC kodovi predstavljaju:
Klasu kodova zasnovanu na matricama provere parnosti sa niskom gustinom
Klasu kodova zasnovanu na matricama provere parnosti sa visokom gustinom
Klasu kodova zasnovanu na verifikacionim matricama provere parnosti
(*)Selektivni ARQ:
Prenosi ponovo samo kodne reci koje sadrze gresku
Prenosi ponovo samo sindrom reci koje sadrze gresku
Prenosi ponovo pojedine kodne reci
Prenosi ponovo sve kodne reci
(*)LDPC kodove je definisao
Robert Gallager
Clode Shannon
Radford Neal
(*)Da li Hemingov kod moze da ispravi sve oblike vektorskih gresaka sa ukupno jednom greskom?
Da
Ne
(*)Verifikaciona matrica kod Hemingovog koda imace uvek nula kolonu I dve iste kolone:
Netacno
Tacno
(*)Ukoliko kodne reci nisu iste duzine:
Ne radi se o blok kodu
Radi se o blok kodu
(*)U uslovima izuzetno velikog suma nije uopste moguce obaviti pouzdan prenos poruka:
Tacno
Netacno
{"name":"Od kviza do kodovanja", "url":"https://www.quiz-maker.com/QPREVIEW","txt":"Testirajte svoje znanje o kodiranju i komunikacionim kanala uz naš interaktivan kviz! Ovaj kviz sadrži 30 pitanja koja pokrivaju razliĝite aspekte kodiranja, ukljuĝujući LDPC kodove, konvolucione kodove, i teoriju informacija.Uĝestvujući u kvizu, nauĝićete:- O znaĝaju kapaciteta kanala - Kako funkcioniraju cikliĝni i blok kodovi - Primjene kodova u razliĝitim tehnologijama","img":"https:/images/course7.png"}