22 Fractals

Fractals are mathematical objects...
These geometric shapes, once enlarged, present more and more subtleties and the enlargement of any part of the object essentially resembles the whole again. The coloring of the fractals serves rather to emphasize and visualize their beauty. Salvador Dali used fractal art in his work "The Face of War" without being their discoverer.

These geometric shapes, once enlarged, present more and more subtleties and the enlargement of any part of the object essentially resembles the whole again. The coloring of the fractals serves rather to emphasize and visualize their beauty. Salvador Dali used fractal art in his work "The Face of War" without being their discoverer.


At the turn of the 19th to the 20th century, the mathematical vision of the world was shaken with the discovery of new structures and geometries that represented extremely counter-intuitive features, such as infinitely fragmented structures with details at all levels. These objects were so "out of the ordinary" that mathematicians of the time compared them to the "chimeras" of Greek mythology and called them "mathematical monsters".
At the turn of the 19th to the 20th century, the mathematical vision of the world was shaken with the discovery of new structures and geometries that represented extremely counter-intuitive features, such as infinitely fragmented structures with details at all levels. These objects were so "out of the ordinary" that mathematicians of the time compared them to the "chimeras" of Greek mythology and called them "mathematical monsters".

The most famous of all fractals is the Mandelbrot set, named after the mathematician Benoît Mandelbrot (1924-2010), who invented the term "fractals" in 1975. Even before the First World War, the French mathematicians Gaston Julia (1893-1978) and Pierre Fatou (1878-1929) developed the mathematical foundations of this set. A first graphical representation was created in 1978 by Robert Brooks and Peter Matelski. Benoît Mandelbrot was working for IBM at the time, and in 1980 he received the first computer visualization of this quantity by means of complex calculations. Through Mandelbrot's authoritative work in fractal geometry, fractals became more and more known and their usefulness for other areas was discovered.
At the LSC you can discover the Mandelbrot set thanks to the application “Retinalmandelbrot” developed by the German mathematician Fritz Hörmann (www.retinalmandelbrot.com).
The most famous of all fractals is the Mandelbrot set, named after the mathematician Benoît Mandelbrot (1924-2010), who invented the term "fractals" in 1975. Even before the First World War, the French mathematicians Gaston Julia (1893-1978) and Pierre Fatou (1878-1929) developed the mathematical foundations of this set. A first graphical representation was created in 1978 by Robert Brooks and Peter Matelski. Benoît Mandelbrot was working for IBM at the time, and in 1980 he received the first computer visualization of this quantity by means of complex calculations. Through Mandelbrot's authoritative work in fractal geometry, fractals became more and more known and their usefulness for other areas was discovered.
At the LSC you can discover the Mandelbrot set thanks to the application “Retinalmandelbrot” developed by the German mathematician Fritz Hörmann (www.retinalmandelbrot.com).

The complex numbers ℂ are an extension of the real numbers ℝ, containing in particular the imaginary number I such that i2 = -1, so the square root of -1 is the correct answer. The cubic root of -1 is -1 and therefore in the set of relative integers ℤ which is a subset of real numbers and the number pi is a real number.
The complex numbers ℂ are an extension of the real numbers ℝ, containing in particular the imaginary number I such that i2 = -1, so the square root of -1 is the correct answer. The cubic root of -1 is -1 and therefore in the set of relative integers ℤ which is a subset of real numbers and the number pi is a real number.

Which of the 3 objects is not perfectly self-similar, which means it does not just consist of reduced copies of itself, regardless of the scale at which it is observed?
The simplest fractals consist of reduced copies of themselves. An example is a perfect tree, whose branches actually have the same shape as the tree itself. These fractals are said to be perfectly self-similar. The tree shown is called the tree of Pythagoras and is constructed using squares.
A straight line is not fractal but also perfectly self-similar because its original structure is maintained by infinite enlargement.
However, the lightning bolt is fractal and has a slightly more complex structure, so that new details appear when zooming in. This set is therefore not perfectly self-similar, but only self-similar. But fractals always show a high degree of self-similarity.
The simplest fractals consist of reduced copies of themselves. An example is a perfect tree, whose branches actually have the same shape as the tree itself. These fractals are said to be perfectly self-similar. The tree shown is called the tree of Pythagoras and is constructed using squares.
A straight line is not fractal but also perfectly self-similar because its original structure is maintained by infinite enlargement.
However, the lightning bolt is fractal and has a slightly more complex structure, so that new details appear when zooming in. This set is therefore not perfectly self-similar, but only self-similar. But fractals always show a high degree of self-similarity.

Starting with a filled triangle, a smaller triangle is removed, whose vertices form the center of the sides of the initial triangle. In the next iteration the same happens with the remaining filled triangles. This is then continued infinitely often, I.e. An infinite removal process.
What is the dimension of the "final triangle”?
A point has dimension 0, a line has dimension 1, a sheet of paper has dimension 2 and a cube has dimension 3. Fractals, on the other hand, can have dimensions that are not integers. We speak of a broken dimension, hence the name fractal, from the Latin "fractus", for breaking.
The initial triangle has dimension 2, of course, but the more often we iterate, the "thinner" our triangle becomes and the closer it gets to an object of dimension 1. This is exactly what the fractal dimension satisfies, by attributing to this triangle, called Sierpinski's triangle, a dimension between 1 and 2, namely 1.59.
A point has dimension 0, a line has dimension 1, a sheet of paper has dimension 2 and a cube has dimension 3. Fractals, on the other hand, can have dimensions that are not integers. We speak of a broken dimension, hence the name fractal, from the Latin "fractus", for breaking.
The initial triangle has dimension 2, of course, but the more often we iterate, the "thinner" our triangle becomes and the closer it gets to an object of dimension 1. This is exactly what the fractal dimension satisfies, by attributing to this triangle, called Sierpinski's triangle, a dimension between 1 and 2, namely 1.59.

Thanks to the fractals...
Invented in 1955 by the Catalan engineer Carlos Puente, the fractal antenna allows the coexistence of several radio technologies such as Bluetooth, WLAN and GPS. Since each of these technologies works in its own frequency range, you would need just as many different antennas. The self-similarity of the fractal antenna makes it possible to have a range with good efficiency for each wavelength.
The fractal structure also adapts to a large edge length in a very small area, so that even relatively long waves can be transmitted or received with a small antenna. This is what has made the compact shape of today's mobile phones possible.
Invented in 1955 by the Catalan engineer Carlos Puente, the fractal antenna allows the coexistence of several radio technologies such as Bluetooth, WLAN and GPS. Since each of these technologies works in its own frequency range, you would need just as many different antennas. The self-similarity of the fractal antenna makes it possible to have a range with good efficiency for each wavelength.
The fractal structure also adapts to a large edge length in a very small area, so that even relatively long waves can be transmitted or received with a small antenna. This is what has made the compact shape of today's mobile phones possible.
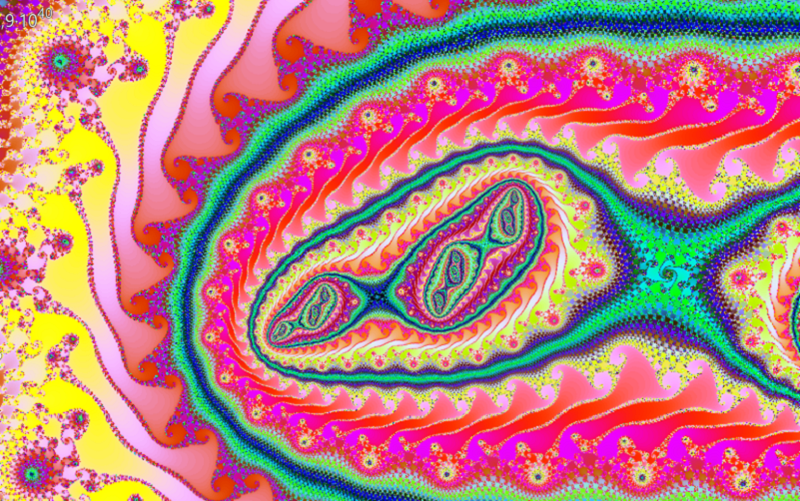
The computer technology of the 80s only made it possible to create simple black and white fractals. This situation changed with the arrival of computers, which are increasingly powerful and capable of performing complex mathematical calculations. They have also made it possible to display fractals in color and to keep the calculation time within limits.
The computer technology of the 80s only made it possible to create simple black and white fractals. This situation changed with the arrival of computers, which are increasingly powerful and capable of performing complex mathematical calculations. They have also made it possible to display fractals in color and to keep the calculation time within limits.

This quiz was written by the Luxembourg Science Center in Differdange. Visit the Centre to learn more about fractals and other scientific topics!
This quiz was written by the Luxembourg Science Center in Differdange. Visit the Centre to learn more about fractals and other scientific topics!
Before you discover your result, please leave us your e-mail address if you would like to be drawn amongst the highest scorers and thereby win free entrances to the Luxembourg Science Center!
Images copyrights :
1 Luxembourg Science Center
2 Luxembourg Science Center
3 Luxembourg Science Center
4 travaux.indse.be
5 wikipedia.org
6 cplusplus.com
7 studydrive.net
8 epo.org
9 Luxembourg Science Center
Images copyrights :
1 Luxembourg Science Center
2 Luxembourg Science Center
3 Luxembourg Science Center
4 travaux.indse.be
5 wikipedia.org
6 cplusplus.com
7 studydrive.net
8 epo.org
9 Luxembourg Science Center