5 Dimensions
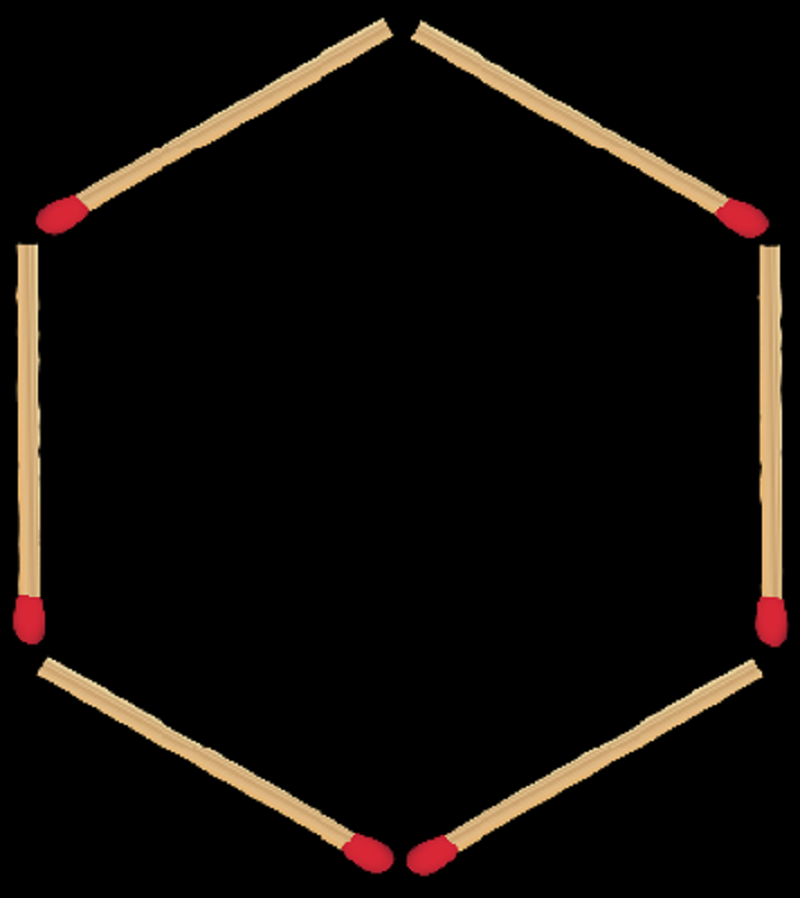
Si on place trois allummettes en forme de Y à l'intérieur de l'hexagone, on obtient une représentation en deux dimensions d'un cube.

Si on place trois allummettes en forme de Y à l'intérieur de l'hexagone, on obtient une représentation en deux dimensions d'un cube.


Qui est l'auteur de la nouvelle satirique "Flatland" ?
„Flatland“ a été écrit en 1884 par l'érudit anglais Edwin Abbott et a été publié sous le pseudonyme "A Square". Le personnage principal, un carré, vie dans un monde plat à deux dimensions et est confronté avec l'existence d'une autre troisième dimension, qui nous est bien familière.
Carl Sagan était un astrophysicien et médiateur scientifique américain qui s'est intéressé entre autres à l'existence possible d'une vie extraterrestre. M.C. Escher était un artiste néerlandais, qui est devenu célèbre grâce à ses représentations de perspectives impossibles.
„Flatland“ a été écrit en 1884 par l'érudit anglais Edwin Abbott et a été publié sous le pseudonyme "A Square". Le personnage principal, un carré, vie dans un monde plat à deux dimensions et est confronté avec l'existence d'une autre troisième dimension, qui nous est bien familière.
Carl Sagan était un astrophysicien et médiateur scientifique américain qui s'est intéressé entre autres à l'existence possible d'une vie extraterrestre. M.C. Escher était un artiste néerlandais, qui est devenu célèbre grâce à ses représentations de perspectives impossibles.

Cette toile de la crucifixion porte le titre de Corpus Hypercubus et montre le Copus Christi sur le patron d'un cube à quatre dimensions aussi appellé "hypercube", d'où le nom de la toile.
Si vous voulez en savoir plus sur le cube Soma ou le Rubik's cube, rendez-vous au Luxembourg Science Center !
Cette toile de la crucifixion porte le titre de Corpus Hypercubus et montre le Copus Christi sur le patron d'un cube à quatre dimensions aussi appellé "hypercube", d'où le nom de la toile.
Si vous voulez en savoir plus sur le cube Soma ou le Rubik's cube, rendez-vous au Luxembourg Science Center !

Existe-t-il des bulles de savon (approximativement) cubiques ?



Quelle théorie physique nécessite plus de trois dimensions spatiales ?
La bonne réponse est la théorie des cordes. Elle fait le pont entre la théorie quantique (le très petit) et la théorie de la gravité (le très grand). Pour réconcilier ces deux concepts fondamentalement différents, il faut des espaces surdimensionnés.
Le modèle standard décrit toutes les particules élémentaires connues et leurs interactions, sans tenir compte de la gravité. La théorie MOND autrement appelé dynamique newtonienne modifiée, est considérée comme une alternative à la matière noire, hypothétique jusqu'à présent.
La bonne réponse est la théorie des cordes. Elle fait le pont entre la théorie quantique (le très petit) et la théorie de la gravité (le très grand). Pour réconcilier ces deux concepts fondamentalement différents, il faut des espaces surdimensionnés.
Le modèle standard décrit toutes les particules élémentaires connues et leurs interactions, sans tenir compte de la gravité. La théorie MOND autrement appelé dynamique newtonienne modifiée, est considérée comme une alternative à la matière noire, hypothétique jusqu'à présent.

La bonne réponse est le corps suivant :

La figure montre comment se forment les ombres du cercle, du carré et du triangle. A partir d'un cylindre, on obtient ce corps en enlevant deux pièces égales par des coupes planes comme sur l'illustration suivante :

La bonne réponse est le corps suivant :

La figure montre comment se forment les ombres du cercle, du carré et du triangle. A partir d'un cylindre, on obtient ce corps en enlevant deux pièces égales par des coupes planes comme sur l'illustration suivante :


Sur quelles trajectoires se déplacent (approximativement) les corps célestes dans notre système solaire ?
A peu près tous les corps célestes du système solaire se déplacent sur des coniques, auxquels appartiennent les cercles, les ellipses, les paraboles et les hyperboles. Tandis que les planètes et leurs lunes tournent sur des trajectoires elliptiques, des comètes se déplacent parfois sur des trajectoires paraboliques, voire hyperboliques.
A peu près tous les corps célestes du système solaire se déplacent sur des coniques, auxquels appartiennent les cercles, les ellipses, les paraboles et les hyperboles. Tandis que les planètes et leurs lunes tournent sur des trajectoires elliptiques, des comètes se déplacent parfois sur des trajectoires paraboliques, voire hyperboliques.

Si on tourne une droite autour d'un axe fixe, on obtient une "hyperboloïde monocoque". Cela permet aux architectes et aux ingénieurs du bâtiment de construire des édifices stables et peu onéreux, puisque l'ensemble de ces structures peut être bâti avec des poutres droites.

Si on tourne une droite autour d'un axe fixe, on obtient une "hyperboloïde monocoque". Cela permet aux architectes et aux ingénieurs du bâtiment de construire des édifices stables et peu onéreux, puisque l'ensemble de ces structures peut être bâti avec des poutres droites.

