22 Fraktale

Fraktale sind mathematische Objekte...
Diese geometrischen Formen, einmal vergrößert, weisen immer mehr Feinheiten auf, und die Vergrößerung eines Teils des Objekts ähnelt im Wesentlichen wieder dem Ganzen. Die Farbgebung der Fraktale dient eher dazu, die Schönheit dieser mathematischen Objekte hervorzuheben. Salvador Dali verwendete die fraktale Kunst in seinem Werk "The Face of War", ohne jedoch der Entdecker zu sein.

Diese geometrischen Formen, einmal vergrößert, weisen immer mehr Feinheiten auf, und die Vergrößerung eines Teils des Objekts ähnelt im Wesentlichen wieder dem Ganzen. Die Farbgebung der Fraktale dient eher dazu, die Schönheit dieser mathematischen Objekte hervorzuheben. Salvador Dali verwendete die fraktale Kunst in seinem Werk "The Face of War", ohne jedoch der Entdecker zu sein.


An der Wende vom 19. zum 20. Jahrhundert wurde das mathematische Weltbild durch die Entdeckung neuer Strukturen und Geometrien erschüttert, die äußerst kontraintuitive Merkmale darstellten, wie z.B. Unendlich fragmentierte Strukturen mit Details auf allen Stufen. Diese Objekte waren so "außergewöhnlich", dass die Mathematiker der damaligen Zeit sie mit den "Chimären" der griechischen Mythologie verglichen und sie als "mathematische Monster" bezeichneten.
An der Wende vom 19. zum 20. Jahrhundert wurde das mathematische Weltbild durch die Entdeckung neuer Strukturen und Geometrien erschüttert, die äußerst kontraintuitive Merkmale darstellten, wie z.B. Unendlich fragmentierte Strukturen mit Details auf allen Stufen. Diese Objekte waren so "außergewöhnlich", dass die Mathematiker der damaligen Zeit sie mit den "Chimären" der griechischen Mythologie verglichen und sie als "mathematische Monster" bezeichneten.

Das berühmteste aller Fraktale ist die Mandelbrot-Menge, benannt nach dem Mathematiker Benoît Mandelbrot (1924-2010), der 1975 den Begriff "Fraktale" erfand. Bereits vor dem Ersten Weltkrieg entwickelten die französischen Mathematiker Gaston Julia (1893-1978) und Pierre Fatou (1878-1929) die mathematischen Grundlagen dieser Menge. Eine erste grafische Darstellung wurde 1978 von Robert Brooks und Peter Matelski geschaffen. Benoît Mandelbrot arbeitete zu dieser Zeit bei IBM und erhielt, im Jahr 1980, mittels aufwendiger Berechnungen eine erste Computervisualisierung dieser Menge. Durch Mandelbrots maßgebende Arbeit in der fraktalen Geometrie, wurden die Fraktale immer bekannter und ihr Nutzen auch für andere Bereiche entdeckt.
Im LSC können Sie die Mandelbrot-Menge entdecken, dank der vom deutschen Mathematiker Fritz Hörmann entwickelten Anwendung „Retinalmandelbrot“ (www.retinalmandelbrot.com).
Das berühmteste aller Fraktale ist die Mandelbrot-Menge, benannt nach dem Mathematiker Benoît Mandelbrot (1924-2010), der 1975 den Begriff "Fraktale" erfand. Bereits vor dem Ersten Weltkrieg entwickelten die französischen Mathematiker Gaston Julia (1893-1978) und Pierre Fatou (1878-1929) die mathematischen Grundlagen dieser Menge. Eine erste grafische Darstellung wurde 1978 von Robert Brooks und Peter Matelski geschaffen. Benoît Mandelbrot arbeitete zu dieser Zeit bei IBM und erhielt, im Jahr 1980, mittels aufwendiger Berechnungen eine erste Computervisualisierung dieser Menge. Durch Mandelbrots maßgebende Arbeit in der fraktalen Geometrie, wurden die Fraktale immer bekannter und ihr Nutzen auch für andere Bereiche entdeckt.
Im LSC können Sie die Mandelbrot-Menge entdecken, dank der vom deutschen Mathematiker Fritz Hörmann entwickelten Anwendung „Retinalmandelbrot“ (www.retinalmandelbrot.com).

Die komplexen Zahlen ℂ sind eine Erweiterung der reellen Zahlen ℝ, die insbesondere die imaginäre Zahl I mit der Eigenschaft i2 = -1 enthält, so dass die Quadratwurzel von -1 die richtige Antwort ist. Die Kubikwurzel von -1 ist -1 und damit in der Menge der ganzen Zahlen ℤ, die eine Teilmenge der reellen Zahlen ist, und die Zahl Pi ist eine reelle Zahl.
Die komplexen Zahlen ℂ sind eine Erweiterung der reellen Zahlen ℝ, die insbesondere die imaginäre Zahl I mit der Eigenschaft i2 = -1 enthält, so dass die Quadratwurzel von -1 die richtige Antwort ist. Die Kubikwurzel von -1 ist -1 und damit in der Menge der ganzen Zahlen ℤ, die eine Teilmenge der reellen Zahlen ist, und die Zahl Pi ist eine reelle Zahl.

Welches der 3 Objekte ist nicht perfekt selbstähnlich, d.h. Es besteht nicht nur aus verkleinerten Kopien seiner Selbst, unabhängig vom Maßstab, in dem es betrachtet wird?
Die einfachsten Fraktale bestehen aus verkleinerten Kopien ihrer Selbst. Ein Beispiel dafür ist ein perfekter Baum, dessen Äste eigentlich wiederum dieselbe Form haben wie der Baum selbst. Solche Fraktale heissen perfekt selbstähnlich. Der abgebildete Baum heißt „Baum des Pythagoras“ und wird mit Hilfe von Quadraten gebildet.
Eine Gerade ist nicht fraktal, jedoch auch perfekt selbstähnlich, weil ihre ursprüngliche Struktur auch durch unendliches Vergrößern erhalten bleibt.
Der Blitz ist wiederum fraktal und hat eine etwas komplexere Struktur, so dass beim Heranzoomen neue Details erscheinen. Dieses Objekt ist also nicht perfekt selbstähnlich, sondern nur selbstähnlich. Die Fraktale weisen nach wie vor immer einen hohen Grad an Selbstähnlichkeit auf.
Die einfachsten Fraktale bestehen aus verkleinerten Kopien ihrer Selbst. Ein Beispiel dafür ist ein perfekter Baum, dessen Äste eigentlich wiederum dieselbe Form haben wie der Baum selbst. Solche Fraktale heissen perfekt selbstähnlich. Der abgebildete Baum heißt „Baum des Pythagoras“ und wird mit Hilfe von Quadraten gebildet.
Eine Gerade ist nicht fraktal, jedoch auch perfekt selbstähnlich, weil ihre ursprüngliche Struktur auch durch unendliches Vergrößern erhalten bleibt.
Der Blitz ist wiederum fraktal und hat eine etwas komplexere Struktur, so dass beim Heranzoomen neue Details erscheinen. Dieses Objekt ist also nicht perfekt selbstähnlich, sondern nur selbstähnlich. Die Fraktale weisen nach wie vor immer einen hohen Grad an Selbstähnlichkeit auf.

Beginnend mit einem gefüllten Dreieck wird ein kleineres Dreieck entfernt, dessen Ecken die Mitte der Seiten des ursprünglichen Dreiecks bilden. Dasselbe wird mit den verbleibenden gefüllten Dreiecken wiederholt. Dies führt man dann unendlich oft fort, also ein unendlicher Entfernungsprozess.
Was ist die Dimension des "endgültigen Dreiecks“?
Ein Punkt hat die Dimension 0, eine Linie die Dimension 1, ein Blatt Papier die Dimension 2 und ein Würfel die Dimension 3. Fraktale hingegen können Dimensionen haben, die keine ganzen Zahlen sind. Wir sprechen von einer gebrochenen Dimension, daher der Name Fraktal, vom lateinischen "fractus", zu brechen.
Das anfängliche Dreieck hat natürlich die Dimension 2, aber je öfter wir iterieren, desto "dünner" wird unser Dreieck und nähert sich einem Objekt der Dimension 1. Und genau das erfüllt die fraktale Dimension, indem sie diesem Dreieck, das Sierpinski-Dreieck genannt wird, eine Dimension zwischen 1 und 2, d.h. 1,59 zuweist.
Ein Punkt hat die Dimension 0, eine Linie die Dimension 1, ein Blatt Papier die Dimension 2 und ein Würfel die Dimension 3. Fraktale hingegen können Dimensionen haben, die keine ganzen Zahlen sind. Wir sprechen von einer gebrochenen Dimension, daher der Name Fraktal, vom lateinischen "fractus", zu brechen.
Das anfängliche Dreieck hat natürlich die Dimension 2, aber je öfter wir iterieren, desto "dünner" wird unser Dreieck und nähert sich einem Objekt der Dimension 1. Und genau das erfüllt die fraktale Dimension, indem sie diesem Dreieck, das Sierpinski-Dreieck genannt wird, eine Dimension zwischen 1 und 2, d.h. 1,59 zuweist.

Dank der Fraktale...
Die 1955 von dem katalanischen Ingenieur Carlos Puente erfundene Fraktalantenne ermöglicht die Koexistenz mehrerer Funktechnologien wie Bluetooth, WLAN und GPS. Da jede dieser Technologien in ihrem eigenen Frequenzbereich arbeitet, wären so viele verschiedene Antennen erforderlich. Die Selbstähnlichkeit der Fraktalantenne ermöglicht einen Bereich mit guter Effizienz für jede Wellenlänge.
Die fraktale Struktur passt sich auch an eine große Kantenlänge in einem sehr kleinen Bereich an, so dass auch relativ lange Wellen mit einer kleinen Antenne gesendet oder empfangen werden können. Dies hat die kompakte Form der heutigen Mobiltelefone erst möglich gemacht.
Die 1955 von dem katalanischen Ingenieur Carlos Puente erfundene Fraktalantenne ermöglicht die Koexistenz mehrerer Funktechnologien wie Bluetooth, WLAN und GPS. Da jede dieser Technologien in ihrem eigenen Frequenzbereich arbeitet, wären so viele verschiedene Antennen erforderlich. Die Selbstähnlichkeit der Fraktalantenne ermöglicht einen Bereich mit guter Effizienz für jede Wellenlänge.
Die fraktale Struktur passt sich auch an eine große Kantenlänge in einem sehr kleinen Bereich an, so dass auch relativ lange Wellen mit einer kleinen Antenne gesendet oder empfangen werden können. Dies hat die kompakte Form der heutigen Mobiltelefone erst möglich gemacht.
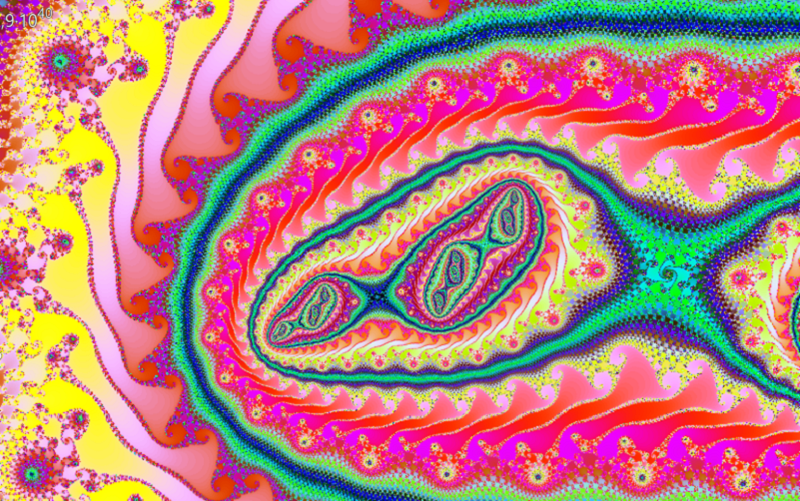
Die Computertechnologie der 80er Jahre erlaubte nur die Erzeugung einfacher Schwarz-Weiß-Fraktale. Diese Situation änderte sich mit dem Aufkommen von Computern, die immer leistungsfähiger wurden und in der Lage waren, komplexe mathematische Berechnungen durchzuführen. Sie machten es auch möglich, Fraktale farbig darzustellen und die Berechnungszeit in Grenzen zu halten.
Die Computertechnologie der 80er Jahre erlaubte nur die Erzeugung einfacher Schwarz-Weiß-Fraktale. Diese Situation änderte sich mit dem Aufkommen von Computern, die immer leistungsfähiger wurden und in der Lage waren, komplexe mathematische Berechnungen durchzuführen. Sie machten es auch möglich, Fraktale farbig darzustellen und die Berechnungszeit in Grenzen zu halten.

Dieses Quiz wurde vom Luxembourg Science Center in Differdingen verfasst. Besuchen sie das Zentrum, um mehr über Fraktale und andere wissenschaftliche Themen zu erfahren!
Dieses Quiz wurde vom Luxembourg Science Center in Differdingen verfasst. Besuchen sie das Zentrum, um mehr über Fraktale und andere wissenschaftliche Themen zu erfahren!
Bevor Sie Ihr Ergebnis entdecken, hinterlassen Sie uns bitte Ihre E-Mail-Adresse. Wir werden verlosen unter den Teilnehmern mit dem höchsten Score gratis Eintritte ins Luxembourg Science Center!
Images copyrights :
1 Luxembourg Science Center
2 Luxembourg Science Center
3 Luxembourg Science Center
4 travaux.indse.be
5 wikipedia.org
6 cplusplus.com
7 studydrive.net
8 epo.org
9 Luxembourg Science Center
Images copyrights :
1 Luxembourg Science Center
2 Luxembourg Science Center
3 Luxembourg Science Center
4 travaux.indse.be
5 wikipedia.org
6 cplusplus.com
7 studydrive.net
8 epo.org
9 Luxembourg Science Center