Grile SI
Neural Network Quiz
Put your knowledge of neural networks to the test with this comprehensive quiz designed for students and professionals alike! Assess your understanding of artificial neurons, activation fun
Key Features:
- 30 multiple choice questions
- Diverse topics covering neural network fundamentals
- Ideal for aspiring data scientists and AI enthusiasts
In modelul neuronal, activarea totala a unui neuron artificial este:
Suma ponderilor marimilor de intrare, minus valoarea de prag
Suma marimilor de intrare ponderate cu valorile ponderilor sinaptice asociate, minus valoarea de prag
Suma marimilor de intrare ponderate cu valorle de prag asociate, minus valorile ponderilor
In modelul neuronal, activarea totala a unui neuron artificial:
Este argumentul funcției neuronale din modelul neuronului artificial
Descrie tipul functiei neuronale
Este valoarea calculata de functia neuronala
In modelul neuronal, ponderile sinaptice:
Pondereaza valorile semnalelor de intrare in calculul activarii totale
Se stabilesc a.î. Activarea totala sa fie mai mica decat valoarea de prag
Modifica valorile semnalelor de intrare pentru a obtine o valoare impusa a semnalui de iesire
In modelul neuronal, ponderile sinaptice:
Pondereaza valorile semnalelor de intrare in calculul activarii totale
Se adapteaza iterativ astfel incat activarea totala sa fie mai mare decat valoarea de prag
Se adapteaza iterativ astfel incat marimea de iesire sa fie mai mica decat o valare maxim admisa
In modelul neuronal, marimea de iesire:
Se obtine prin calcularea valorii functiei neuronale pe baza activarii totale
Se modifica doar cand valoarea activarii totale depaseste valoarea unui prag
Se obtine prin modificarea ponderilor sinaptice pe baza unui algoritm de antrenare
In modelul neuronal, un semnal de intrare este conditionat de:
Valoarea activarii totale a neuronului artificial
Valoarea ponderii sinaptice asociata semnalului respectiv
Valoarea erorii de antrenare la iteratia curenta a algoritmului de antrenare
Care dintre urmatoarele sunt functii neuronale uzuale:
Functia criteriu pentru minimizarea erorii de antrenare
Functia prag asimetric
Functia de activare de tip trapezoidal
Care dintre urmatoarele sunt functii neuronale uzuale?
Functia semn (signum)
Functia de activare de tip triunghiular
Functia de transfer
Care dintre urmatoarele sunt functii neuronale uzuale:
Functia de activare de tip trapezoidal
Functia gaussiana
Functia liniara cu limitare simetrica
Care dintre urmatoarele sunt functii neuronale uzuale:
Functia impuls dirac
Functia liniara
Functia criteriu pentru minimizarea erorii de antrenare
In cazul algoritmilor de antrenare supervizata:
Datele de antrenare contin valori pentru marimile de intrare ale retelei si valori corespunzatoare pentru marimile de iesire
Datele de antrenare contin valori pentru marimile de intrare ale retelei si valori corespunzatoare pentru ponderile sinaptice ale acestora
Datele de antrenare contin valorile initiale pentru ponderile sinaptice ale retelei si valori corespunzatare pentru marimile de iesire
La antrenarea supervizata:
Se poate defini o eroare de antrenare ca diferenta dintre valoarea curenta a functiei criteriu și valoarea curenta a acesteia
Se poate defini o eroare de antrenare ca diferenta dintre valorile impuse ale marimilor de iesire și valorile curente ale acestora la fiecare iteratie
Se poate defini o eroare de antrenare ca diferenta dintre valorile optime ale ponderilor sinaptice si valorile curente ale acestora la fiecare iteratie
In cazul algoritmilor de antrenare nesupervizata:
Datele de antrenare contin valorile optime ale ponderilor sinaptice astfel incat nu mai este necesara supervizarea antrenarii
Datele de antrenare contin valori pentru marimile de intrare ale retelei si valori corespunzatoare pentru marimile de iesire
Datele de antrenare contin doar valori ale semnalelor de intrare ale retelei
La algoritmul perceptronului, relatia de adaptare iterativa a valorii ponderii sinaptice a semnalului de intrare 𝑖 este de forma (semnificatia notatiilor este cea din suportul de curs):
Н��𝑖𝑘+1=𝑤𝑖𝑘+𝑝(𝑑𝑘−𝑦𝑘)
Н��𝑖𝑘+1=Σ𝑤𝑖𝑘𝑛𝑖=1𝑥𝑖𝑘−𝑝
Н��𝑖𝑘+1=𝑤𝑖𝑘+𝑝(𝑑𝑘−𝑦𝑘)𝑥𝑖𝑘
In modelul perceptronului:
Functia neuronala returneaza o valoare dintr-o mulțime finita , de obicei fiind 0 sau 1
Valoarea de prag poate fi 0 sau 1
Activarea totala este calculata doar daca semnalele de intrare depasesc un anumit prag
La algoritmul perceptronului, in varianta sa initiala, conditia de oprire este:
Eroarea totala de antrenare la iteratia curenta este mai mica de o valoare maxim admisa
Nici o pondere nu se modifica pentru P iteratii consecutive, unde P este numarul de perechi de date de antrenare distincte
Nici o pondere nu se modifica pentru P iteratii consecutive, unde P este un numar ales initial pe baza experientei
In modelul perceptronului:
Functia neuronala specifica este functia prag (simetric sau asimetric)
Nu are o functie neuronala specifica
Functia neuronala specifica este functia liniara
Retelele de tip perceptron se pot folosi in probleme de:
Prelucrare a seriilor de timp
Regresie liniara
Clasificare a datelor de antrenare
Pentru a utiliza algoritmul standard de antrenare al perceptronului:
Datele de antrenare trebuie sa fie mai mari de o valoare de prag
Datele de antrenare trebuie sa fie mai mici de o valoare maxim admisa
Datele de antrenare trebuie sa fie liniar separabile
Algoritmul de antrenare al perceptronului este:
Un algoritm de antrenare supervizatata
Un algoritm de antrenare convergent
Un algoritm de antrenare nesupervizatata
Retelele de tip perceptron se pot folosi in probleme de:
Prelucrare a seriilor de timp
Clasificare a datelor de antrenare
Regresie liniara
Algoritmul de antrenare al retelelor neuronale liniare este:
Un algoritm de antrenare supervizata
Un algoritm de antrenare optima
Un algoritm de antrenare nesupervizata
Retelele neuronale liniare se pot folosi in probleme de:
Interferenta fuzzy
Clasificare a datelor de antrenare
Regresie liniara
In modelul neuronului liniar:
Valoarea de prag se calculeaza din valorile semnalelor de intrare printr-o relatie liniara
Functia neuronala returneaza o valoare dintr-un sub-domeniu de valori din multimea numerelor reale
Valorile ponderilor sinaptice pot fi folosite la trasarea unei linii care separa datele de antrenare
La algoritmul de antrenare al retelelor liniare, relatia de adaptare iterativa a valorii ponderii sinaptice a semnalului de intrare 𝑖 este de forma:
Н��𝑖𝑘+1=Σ𝑤𝑖𝑘𝑛𝑖=1𝑥𝑖𝑘−𝑝
Н��𝑖𝑘+1=𝑤𝑖𝑘+𝑝(𝑑𝑘−𝑦𝑘)
Н��𝑖𝑘+1=𝑤𝑖𝑘+𝑝(𝑑𝑘−𝑦𝑘)𝑥𝑖𝑘
In modelul neuronului liniar:
Functia neuronala specifica este functia de prag
Functia neuronala specifica este functia liniara (cu sau fara limitare)
Nu are o functie neuronala specifica
La algoritmul de antrenare al retelelor liniare, conditia de oprire este:
Eroarea totala de antrenare la iteratia curenta este mai mica de o valoare maxim admisa
Nici o pondere nu se modifica pentru P iteratii consecutive, unde P este numarul de perechi de date de antrenare distincte
Eroarea totala de antrenare este mai mica de o valoare maxim admisa pentru P iteratii consecutive, unde P este numarul de antrenare distincte
?Pentru algoritmul de antrenare al retelelor liniare:
Datele de antrenare trebuie sa fie liniar separabile
Datele de antrenare pot fi afectate de erori fiindca acestea nu conduc la blocarea algoritmului
Datele de antrenare nu trebuie sa contina erori deoarece erorile conduc la blocarea algoritmului
In cazul retelelor neurale unidirectionale multistrat:
Semnalele de activare pargurg reteaua de la intrare catre iesire, iar semnalele de iesire parcurg reteaua de la iesire catre intrare
Semnalele parcurg reteaua doar de la intrare spre iesire
Unitatile functionale sunt organizate pe straturi pentru a asigura convergenta algoritmilor de antrenare
Caracteristicile retelelor neuronale unidirectionale multistrat sunt:
Unitatile functionale sunt organizate pe doua straturi, astfel incat toti neuronii sunt conectati fiecare cu fiecare
Unitatile functionale pot avea functii neuronale derivabile (functia liniara sau functia sigmoidala)
Unitatile functionale se pot grupa pe straturi astfel incat sa nu avem conexiuni intre neuroni aflati pe acelasi strat si nici conexiuni de la neuronii de pe un strat catre neuronii aflati pe un strat anterior
In cazul retelelor neuronale unidirectionale multistrat:
Nu exista conexiuni intre neuronii aflati pe stratul ascuns si cei aflati pe stratul de iesire
Intrarile neuronilor de pe stratul ascuns sunt iesiri ale neuronilor de pe stratul de iesire al retelei multistrat
Iesirile neuronilor de pe stratul ascuns sunt intrari ale neuronilor de pe stratul de iesire al retelei multistrat
Metoda propagarii inapoi a erorii este:
Un algoritm de antrenare nesupervizata a retelelor multistrat
Un algoritm de antrenare a retelelor multistrat prin care reteaua este antrenata invers
Un algoritm de antrenare supervizata a retelelor multistrat
La metoda propagarii inapoi a erorii:
Eroarea de antrenare dinamica pentru fiecare unitate functionala este calculata in ordinea inversa a straturilor de neuroni, incepand cu neuronii ultimului strat
Activarile totale ale neuronilor sunt calculate in ordinea inversa a straturilor de neuroni, incepand cu neuronii ultimului strat
Semnalele parcurg reteaua in ordinea inversa a straturilor de neuroni, incepand cu neuronii ultimului strat
Tipurile fundamentale de antrenare a retelelor neuronale sunt:
Supervizata si nesupervizata
Iterativa si intr-o singura etapa
Convergenta si neconvergenta
Instruirea retelelor neuronale consta in:
Adaptarea iterativa a valorilor ponderilor sinaptice pe baza unui set de date de antrenare
Calcularea valorilor ponderilor sinaptice pe baza valorilor datelor de antrenare care indeplinesc anumite conditii
Alegerea valorilor ponderilor sinaptice pentru obtinerea unei valori minime a erorii de antrenare
?Categoria fundamentala a unui algoritm de antrenare:
Este data de structura setului de date de antrenare
Este stabilita de disponibilitatea unui supervizor care sa urmareasca evolutia antrenarii
Este data de tipul functiei neuronale
Urmatoarele functii de apartenenta sunt definite pe intervalul [-21,21] pentru variabila fuzzy 𝑢:
𝜇𝑝𝝵(𝑢)=𝝿(𝑢,−19,−17)
𝜇𝑝𝑀(𝑢)=𝜋(𝑢,−19,−17,−8,−7)
𝜇𝑝𝑆(𝑢)=𝜋(𝑢,−8,−7,−1,0)
𝜇𝑝𝝸(𝑢)=Δ(𝑢,−1,0,1)
𝜇𝑃𝑆(𝑢)=𝜋(𝑢,0,1,7,8)
𝜇𝑃𝑀(𝑢)=𝜋(𝑢,7,8,17,19)
𝜇𝑃𝝵(𝑢)=Г(𝑢,17,19)
La momentul prezent 𝑢=7.25. Calculati gradele de apartenenta ale lui 𝑢, selectand una din optiunile:
Н��𝑝𝝵=0, 𝜇𝑝𝑀=0, 𝜇𝑝𝑆=0, 𝜇𝑝𝝸=0,𝜇𝑃𝑆=0.25, 𝜇𝑃𝑀=0.5, 𝜇𝑃𝝵=0
Н��𝑝𝝵=0, 𝜇𝑝𝑀=0, 𝜇𝑝𝑆=0, 𝜇𝑝𝝸=0,𝜇𝑃𝑆=0.5, 𝜇𝑃𝑀=0.25, 𝜇𝑃𝝵=0
Н��𝑝𝝵=0, 𝜇𝑝𝑀=0, 𝜇𝑝𝑆=0, 𝜇𝑝𝝸=0.5,𝜇𝑃𝑆=0.5, 𝜇𝑃𝑀=0.5, 𝜇𝑃𝝵=0
Н��𝑝𝝵=0, 𝜇𝑝𝑀=0, 𝜇𝑝𝑆=0, 𝜇𝑝𝝸=0,𝜇𝑃𝑆=0.75, 𝜇𝑃𝑀=0.25, 𝜇𝑃𝝵=0
Н��𝑝𝝵=0, 𝜇𝑝𝑀=0, 𝜇𝑝𝑆=0, 𝜇𝑝𝝸=0,𝜇𝑃𝑆=0.25, 𝜇𝑃𝑀=0.75, 𝜇𝑃𝝵=0
Urmatoarele funcții de apartenenta sunt definite pe intervalul [-19,19] pentru variabila fuzzy 𝑢:
𝜇𝑝𝝵(𝑢)=𝝿(𝑢,−18,−16)
𝜇𝑝𝑀(𝑢)=𝜋(𝑢,−18,−16,−8.5,−5.5)
𝜇𝑝𝑆(𝑢)=𝜋(𝑢,−8.5,−6,−1,0)
𝜇𝑝𝝸(𝑢)=Δ(𝑢,−1,0,1)
𝜇𝑃𝑆(𝑢)=𝜋(𝑢,0,1,6,8.5)
𝜇𝑃𝑀(𝑢)=𝜋(𝑢,5.5,8.5,16,18)
𝜇𝑃𝝵(𝑢)=Г(𝑢,16,18)
La momentul prezent 𝑢=−8. Calculati gradele de apartenenta ale lui 𝑢, selectand una din optiunile:
Н��𝑝𝝵=0, 𝜇𝑝𝑀=0, 𝜇𝑝𝑆=0.2, 𝜇𝑝𝝸=0.83,𝜇𝑃𝑆=0, 𝜇𝑃𝑀=0, 𝜇𝑃𝝵=0
Н��𝑝𝝵=0, 𝜇𝑝𝑀=0.83, 𝜇𝑝𝑆=0.2, 𝜇𝑝𝝸=0,𝜇𝑃𝑆=0, 𝜇𝑃𝑀=0, 𝜇𝑃𝝵=0
Н��𝑝𝝵=0, 𝜇𝑝𝑀=0.16, 𝜇𝑝𝑆=0.83, 𝜇𝑝𝝸=0,𝜇𝑃𝑆=0, 𝜇𝑃𝑀=0, 𝜇𝑃𝝵=0
Н��𝑝𝝵=0, 𝜇𝑝𝑀=0, 𝜇𝑝𝑆=0.83, 𝜇𝑝𝝸=0.16,𝜇𝑃𝑆=0, 𝜇𝑃𝑀=0, 𝜇𝑃𝝵=0
Н��𝑝𝝵=0, 𝜇𝑝𝑀=0.83, 𝜇𝑝𝑆=0.16, 𝜇𝑝𝝸=0.5,𝜇𝑃𝑆=0, 𝜇𝑃𝑀=0, 𝜇𝑃𝝵=0
Un controller cu 2 intrari, 𝑒 si Δ𝑒, si o iesire Δ𝑢 ,are definite pentru ieșirea Δ𝑢 următoarele valori fuzzy cu funcțiile de apartenenta associate pe universul de discurs [-21,21]:
𝜇𝑝𝝵(Δ𝑢)=𝝿(Δ𝑢,−19,−17)
𝜇𝑝𝑀(Δ𝑢)=𝜋(Δ𝑢,−19,−17,−8,−7)
𝜇𝑝𝑆(Δ𝑢)=𝜋(Δ𝑢,−8,−7,−1,0)
𝜇𝑝𝝸(Δ𝑢)=Δ(Δ𝑢,−1,0,1)
𝜇𝑃𝑆(Δ𝑢)=𝜋(Δ𝑢,0,1,7,8)
𝜇𝑃𝑀(Δ𝑢)=𝜋(Δ𝑢,7,8,17,19)
𝜇𝑃𝝵(Δ𝑢)=Г(Δ𝑢,17,19)
Ca urmare a proceselor de fuzzificare și inferenta din cadrul controller-ului, a rezultat urmatoarea tabela de inferenta pentru Δ𝑢:
𝑝𝝸 0.5 𝑃𝑆 0.7
𝑃𝑆 0.5 𝑃𝑀 0.7
Folosind metoda de defuzzificare a primului maxim, calculați valoarea lui Δ𝑢 si selectati raspunsul corespunzător.
0.7
-0.5
17.6
4
7.7
Un controller fuzzy cu 2 intrari, 𝑒 si Δ𝑒, si o iesire Δ𝑢 are definite pentru iesirea Δ𝑢 urmatoarele valori fuzzy cu funcțiile de apartenentă associate pe universul de discurs [-19,19]:
𝜇𝑝𝝵(𝑢)=𝝿(𝑢,−18,−16)
𝜇𝑝𝑀(𝑢)=𝜋(𝑢,−18,−16,−8.5,−5.5)
𝜇𝑝𝑆(𝑢)=𝜋(𝑢,−8.5,−6,−1,0)
𝜇𝑝𝝸(𝑢)=Δ(𝑢,−1,0,1)
𝜇𝑃𝑆(𝑢)=𝜋(𝑢,0,1,6,8.5)
𝜇𝑃𝑀(𝑢)=𝜋(𝑢,5.5,8.5,16,18)
𝜇𝑃𝝵(𝑢)=Г(𝑢,16,18)
Ca urmare a proceselor de fuzzificare și inferenta din cadrul controller-ului, a rezultat urmatoarea tabelă de inferenta pentru Δ𝑢:
𝑃𝑆 0.5 𝑃𝑀 0.7
𝑃𝑀 0.5 𝑃𝝵 0.7
Folosind metoda de defuzzificare a inaltimii, calculati valoarea lui Δ𝑢 și selectați raspunsul corespunzator.
11.20
12.13
12.83
-11.25
11.75
Un controller cu 2 intrari, 𝑒 si Δ𝑒, si o iesire Δ𝑢 ,are definite pentru ieșirea Δ𝑢 următoarele valori fuzzy cu funcțiile de apartenenta associate pe universul de discurs [-21,21]:
𝜇𝑝𝝵(Δ𝑢)=𝝿(Δ𝑢,−19,−17)
𝜇𝑝𝑀(Δ𝑢)=𝜋(Δ𝑢,−19,−17,−8,−7)
𝜇𝑝𝑆(Δ𝑢)=𝜋(Δ𝑢,−8,−7,−1,0)
𝜇𝑝𝝸(Δ𝑢)=Δ(Δ𝑢,−1,0,1)
𝜇𝑃𝑆(Δ𝑢)=𝜋(Δ𝑢,0,1,7,8)
𝜇𝑃𝑀(Δ𝑢)=𝜋(Δ𝑢,7,8,17,19)
𝜇𝑃𝝵(Δ𝑢)=Г(Δ𝑢,17,19)
Ca urmare a proceselor de fuzzificare și inferenta din cadrul controller-ului, a rezultat urmatoarea tabela de inferenta pentru Δ𝑢:
𝑝𝑆 0.4 𝑝𝝸 0.5
𝑝𝝸 0.4 𝑃𝑆 0.5
Folosind metoda de defuzzificare mijlocul maximelor, calculati valoarea lui Δ𝑢 si selectati raspunsul corespunzător.
7.5
0
4
3.5
-0.5
Un controller cu 2 intrari, 𝑒 si Δ𝑒, si o iesire Δ𝑢 ,are definite pentru ieșirea Δ𝑢 următoarele valori fuzzy cu funcțiile de apartenenta associate pe universul de discurs [-21,21]:
𝜇𝑝𝝵(Δ𝑢)=𝝿(Δ𝑢,−19,−17)
𝜇𝑝𝑀(Δ𝑢)=𝜋(Δ𝑢,−19,−17,−8,−7)
𝜇𝑝𝑆(Δ𝑢)=𝜋(Δ𝑢,−8,−7,−1,0)
𝜇𝑝𝝸(Δ𝑢)=Δ(Δ𝑢,−1,0,1)
𝜇𝑃𝑆(Δ𝑢)=𝜋(Δ𝑢,0,1,7,8)
𝜇𝑃𝑀(Δ𝑢)=𝜋(Δ𝑢,7,8,17,19)
𝜇𝑃𝝵(Δ𝑢)=Г(Δ𝑢,17,19)
Ca urmare a proceselor de fuzzificare și inferenta din cadrul controller-ului, a rezultat urmatoarea tabela de inferenta pentru Δ𝑢:
𝑝𝑆 0.5 𝑝𝝸 0.7
𝑝𝝸 0.5 𝑃𝑆 0.7
Folosind metoda de defuzzificare mijlocul maximelor, calculati valoarea lui Δ𝑢 si selectati raspunsul corespunzător.
7.5
0
4
3.5
-0.5
Un controller fuzzy cu 2 intrari, 𝑒 si Δ𝑒, si o iesire Δ𝑢 are definite pentru iesirea Δ𝑢 urmatoarele valori fuzzy cu funcțiile de apartenentă associate pe universul de discurs [-19,19]:
𝜇𝑝𝝵(𝑢)=𝝿(𝑢,−18,−16)
𝜇𝑝𝑀(𝑢)=𝜋(𝑢,−18,−16,−8.5,−5.5)
𝜇𝑝𝑆(𝑢)=𝜋(𝑢,−8.5,−6,−1,0)
𝜇𝑝𝝸(𝑢)=Δ(𝑢,−1,0,1)
𝜇𝑃𝑆(𝑢)=𝜋(𝑢,0,1,6,8.5)
𝜇𝑃𝑀(𝑢)=𝜋(𝑢,5.5,8.5,16,18)
𝜇𝑃𝝵(𝑢)=Г(𝑢,16,18)
Ca urmare a proceselor de fuzzificare și inferenta din cadrul controller-ului, a rezultat urmatoarea tabelă de inferenta pentru Δ𝑢:
𝑃𝑆 0.5 𝑃𝑀 0.7
𝑃𝑀 0.5 𝑃𝝵 0.7
Folosind metoda de defuzzificare a inaltimii, calculati valoarea lui Δ𝑢 și selectați raspunsul corespunzator.
12.26
12.83
13.2
-11.25
11.75
Specificati semnificatia elementului structurii: LX
Setul de valori lingvistice pe care-l poate lua X
Functia care face legatura intre valorile lingvistice fuzzy cu valorile cantitative
Numele simbolic al variabilei lingvistice
Domeniul de valori clasice in care variaza variabila lingvistica
Specificati semnificatia elementului structurii: Mx
Setul de valori lingvistice pe care-l poate lua X
Functia care face legatura intre valorile lingvistice fuzzy cu valorile cantitative
Numele simbolic al variabilei lingvistice
Domeniul de valori clasice in care variaza variabila lingvistica
Specificati semnificatia elementului structurii: X
Setul de valori lingvistice pe care-l poate lua X
Functia care face legatura intre valorile lingvistice fuzzy cu valorile cantitative
Numele simbolic al variabilei lingvistice
Domeniul de valori clasice in care variaza variabila lingvistica
Specificati semnificatia elementului structurii: X``
Setul de valori lingvistice pe care-l poate lua X
Functia care face legatura intre valorile lingvistice fuzzy cu valorile cantitative
Numele simbolic al variabilei lingvistice
Domeniul de valori clasice in care variaza variabila lingvistica
Metoda mijlocul maximelor
Metoda sumei
Metoda primului maxim
Metoda inaltimii
Metoda ultimulu maxim
Metoda centrului de greutate
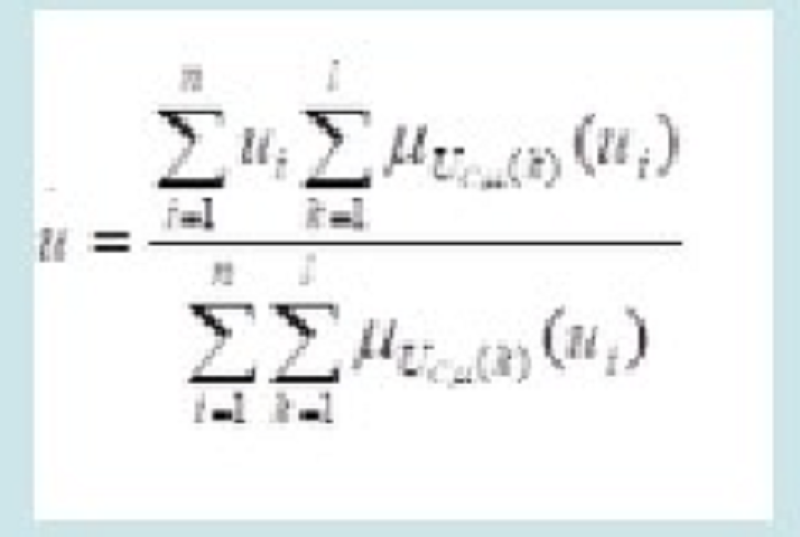
Metoda mijlocul maximelor
Metoda sumei
Metoda primului maxim
Metoda inaltimii
Metoda ultimului maxim
Metoda centrului de greutate
Metoda mijlocul maximelor
Metoda sumei
Metoda primului maxim
Metoda inaltimii
Metoda ultimului maxim
Metoda centrului de greutate
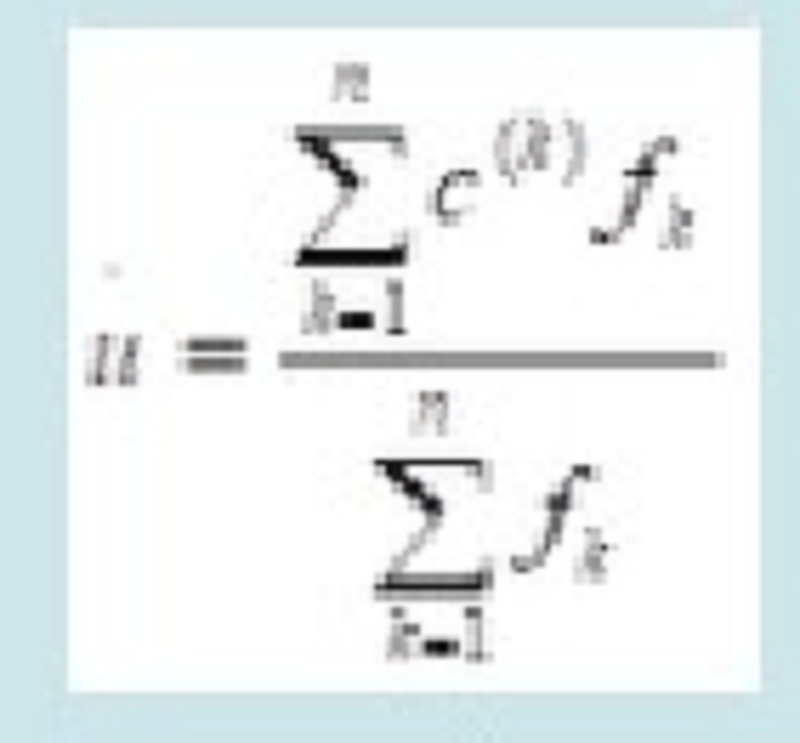
Metoda mijlocul maximelor
Metoda sumei
Metoda primului maxim
Metoda inaltimii
Metoda ultimului maxim
Metoda centrului de greutate
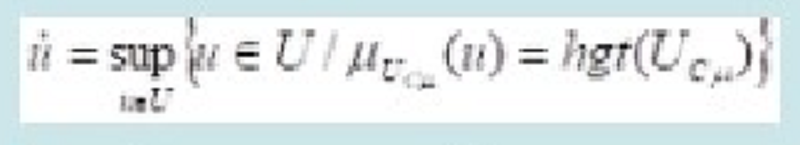
Metoda mijlocul maximelor
Metoda sumei
Metoda primului maxim
Metoda inaltimii
Metoda ultimului maxim
Metoda centrului de greutate
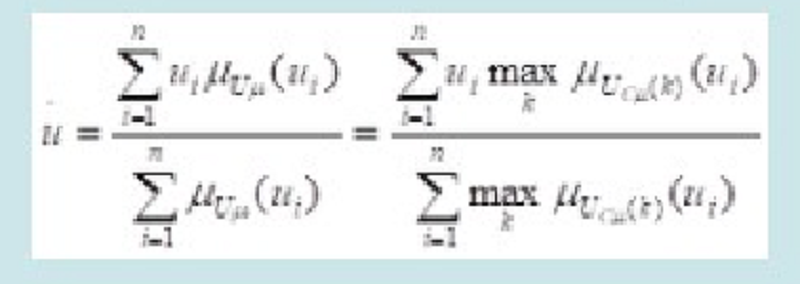
Metoda mijlocul maximelor
Metoda sumei
Metoda primului maxim
Metoda inaltimii
Metoda ultimului maxim
Metoda centrului de greutate
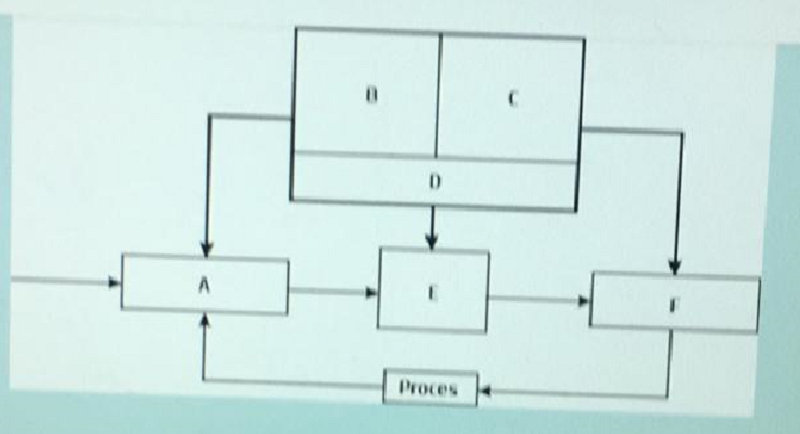
Ce este A ?
Modulul de fuzzificare
Functiile de apartenenta pentru variabilele de intrare
Functiile de apartenenta pentru variabilele de iesire
Baza de reguli
Motor de inferenta
Modulul de defuzzificare
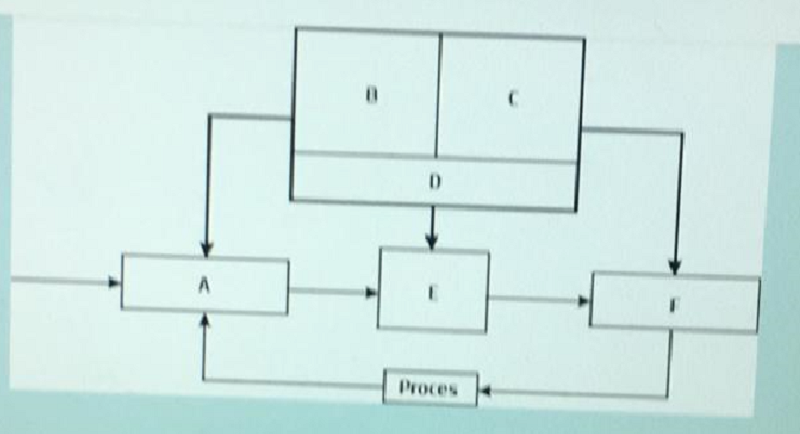
Ce este B ?
Modulul de fuzzificare
Functiile de apartenenta pentru variabilele de intrare
Functiile de apartenenta pentru variabilele de iesire
Baza de reguli
Motor de inferenta
Modulul de defuzzificare
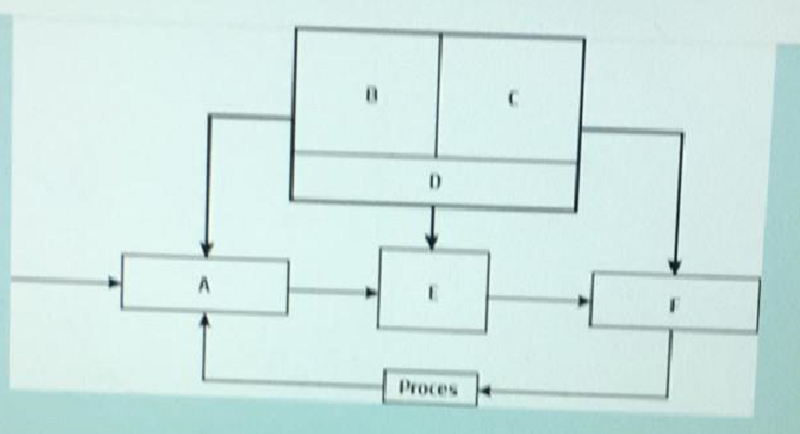
Ce este C ?
Modulul de fuzzificare
Functiile de apartenenta pentru variabilele de intrare
Functiile de apartenenta pentru variabilele de iesire
Baza de reguli
Motor de inferenta
Modulul de defuzzificare
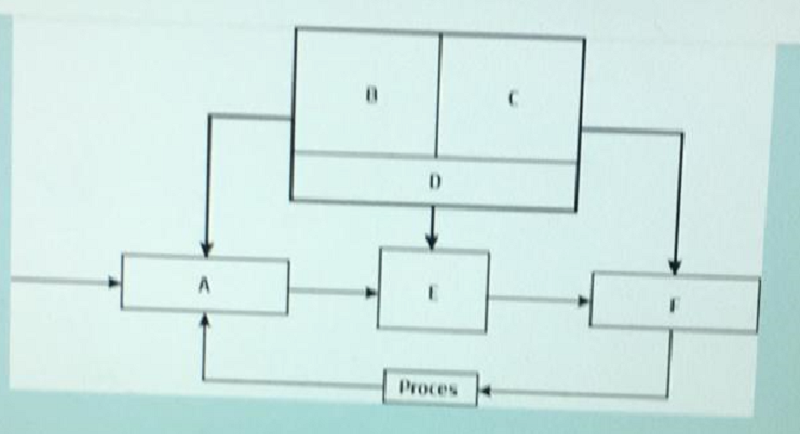
Ce este D ?
Modulul de fuzzificare
Functiile de apartenenta pentru variabilele de intrare
Functiile de apartenenta pentru variabilele de iesire
Baza de reguli
Motor de inferenta
Modulul de defuzzificare
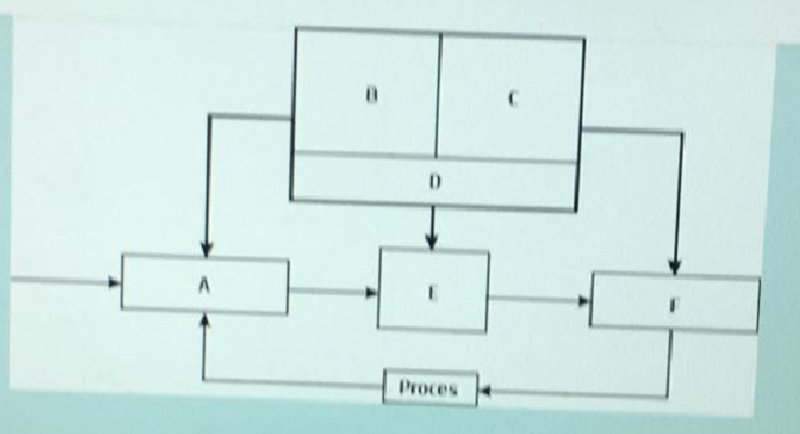
Ce este E ?
Modulul de fuzzificare
Functiile de apartenenta pentru variabilele de intrare
Functiile de apartenenta pentru variabilele de iesire
Baza de reguli
Motor de inferenta
Modulul de defuzzificare
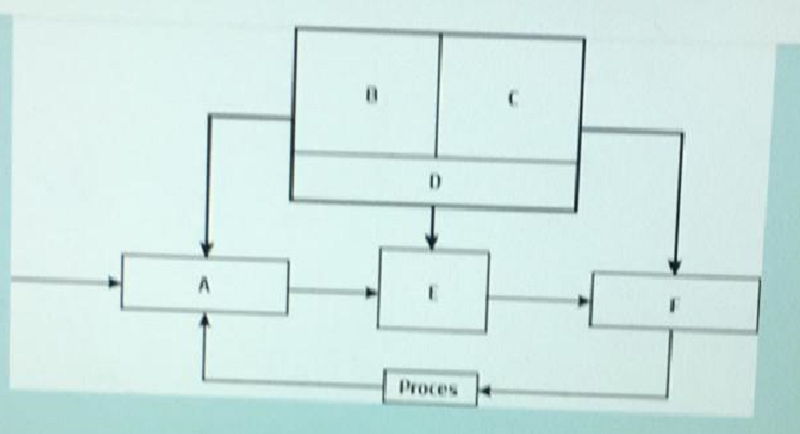
Ce este F ?
Modulul de fuzzificare
Functiile de apartenenta pentru variabilele de intrare
Functiile de apartenenta pentru variabilele de iesire
Baza de reguli
Motor de inferenta
Modulul de defuzzificare
{"name":"Grile SI", "url":"https://www.quiz-maker.com/QPREVIEW","txt":"Put your knowledge of neural networks to the test with this comprehensive quiz designed for students and professionals alike! Assess your understanding of artificial neurons, activation functions, training algorithms, and more.Key Features:30 multiple choice questionsDiverse topics covering neural network fundamentalsIdeal for aspiring data scientists and AI enthusiasts","img":"https:/images/course4.png"}